光の速さを１とする単位系を用います。
横軸（ x 軸 ）が空間で縦軸（ y 軸 ）が時間の２次元時空間で考えてください。


（１） ローレンツ変換の具体例

Ａ君は物質Ｄが速さ 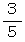で等速直線運動しているのを観察しています。
Ｂ君は物質Ｄと常に同じ場所に存在します。
観察時刻 ０目 には、 Ａ君とＢ君と物質Ｄと光子は同じ場所に位置していました。

観察時刻 １目 には、 Ｂ君と物質ＤはＡ君の２次元時空間座標系では、 次の位置に存在します。
　　　
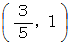
これをＢ君の座標系に座標変換します。
　　　
　　　

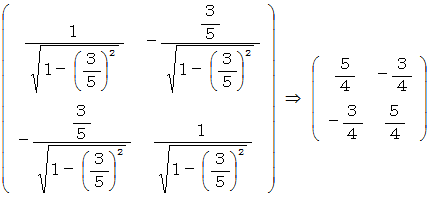
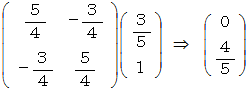
観察時刻 １目 には、 光子はＡ君の２次元時空間座標系では、 次の位置に存在します。
　　　
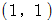
これをＢ君の座標系に座標変換します。
　　　

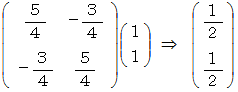
以上の２つをまとめて図にすると、 次のようになります。

　　　

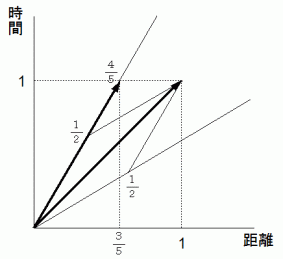
　　　（ 追伸 ）
　　　　　　　　特殊相対性理論の土台になっている 「 ローレンツ座標変換 」 は、 空間を
　　　　　　　１次元とした２次元時空間座標系においては、 縦軸は 「 絶対時間 」であり、
　　　　　　　直交座標系から斜交座標系への座標変換です。

　　　　　　　　ローレンツ変換（ ローレンツ座標変換 ）：
　　　　　　　　　( 固有時間 )^２　＝　( 絶対時間 )^２　−　( 移動空間 )^２
　　　　　　　　　座標変換で 固有時間は不変

（２） ばいおりんの慣性系相対性理論の座標変換

　 私の提唱する座標変換は、 縦軸は 「 相対時間 」 であり、 直交座標系から直交座標系への座標変換です。 私の提唱する座標変換は、 座標軸を の角度だけ反時計回りに回転させるという座標変換です。
　　　


たとえば、 ｖ_２ ＝ −１ × ｖ_１ のときは、 Ｖ ＝ ０ になるので、 次のようになります。

　　　

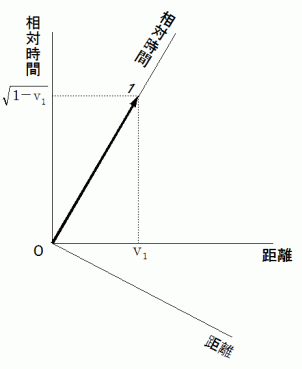
また、 ｖ_１ ＝ １ のときは、 Ｖ ＝ １ になるので、 次のようになります。

　　　


　　　（ 追伸 ）
　　　　　　　　私説の座標変換 ：
　　　　　　　　　　( 絶対時間 )^２　＝　( 相対時間 )^２　＋　( 移動空間 )^２
　　　　　　　　　　座標変換で 絶対時間は不変