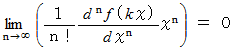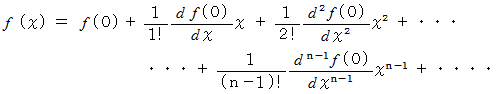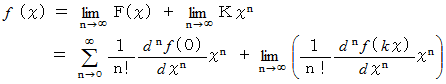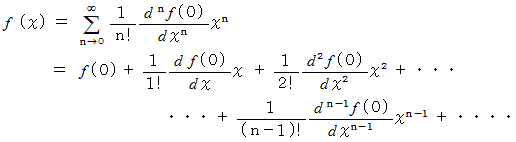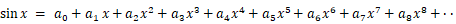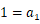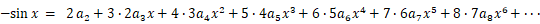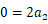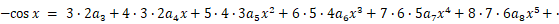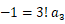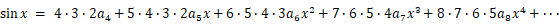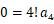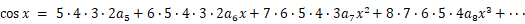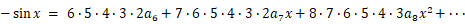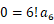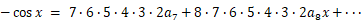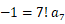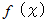 が
が 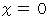 を含む区間で
を含む区間で  回 微分可能であるならば、 この区間内で、
回 微分可能であるならば、 この区間内で、 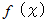 は次のように表されます。 これを 「 マクローリンの定理 」 といいます。
は次のように表されます。 これを 「 マクローリンの定理 」 といいます。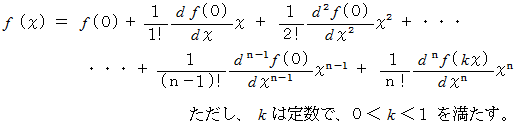
( 証 明 )
-
見やすくするために、 マクローリンの定理を表す式を、 次のように置きます。
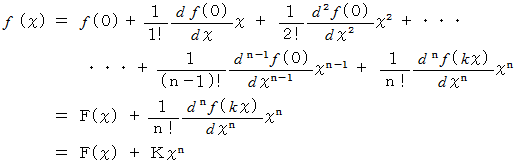
次のように表される関数
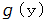 を考えます。
を考えます。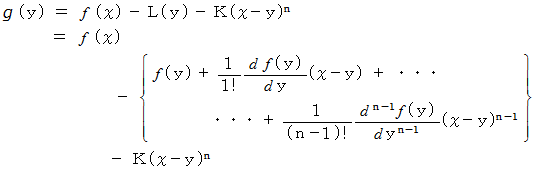
すると、
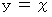 のときは、 次の式が成り立ちます。
のときは、 次の式が成り立ちます。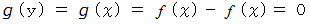
また、
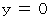 のときは、 次の式が成り立ちます。
のときは、 次の式が成り立ちます。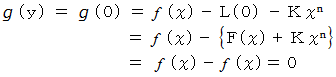
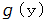 は
は  以上
以上  以下の区間においてで微分可能です。 また、 上記の2つの式が成り立っているので、
以下の区間においてで微分可能です。 また、 上記の2つの式が成り立っているので、  以上
以上  以下の区間で次の式を満たす
以下の区間で次の式を満たす  が存在します。
が存在します。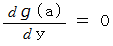
さて、
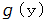 を
を  で微分すると、 次のようになります。
で微分すると、 次のようになります。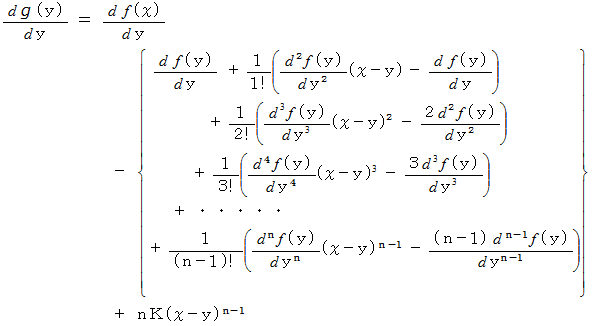
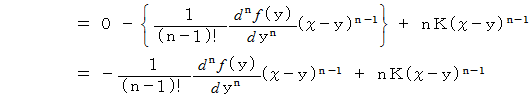
したがって、
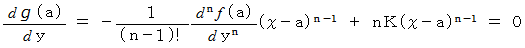
ここで、
 ですから、 次の式が成り立ちます。
ですから、 次の式が成り立ちます。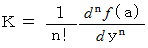
ここで、
 ですから、 次のように
ですから、 次のように  を置き直すことができます。
を置き直すことができます。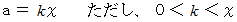
すると
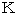 は次のようになります。
は次のようになります。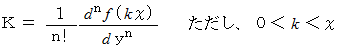
これは、 最初に定義した
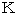 と同じですので、 整合性があります。 したがって、
と同じですので、 整合性があります。 したがって、 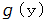 は次のように表されます。
は次のように表されます。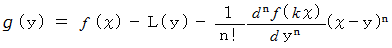
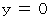 のとき、 上の式は次のようになります。
のとき、 上の式は次のようになります。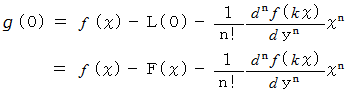
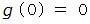 でしたので、 上の式は次のようになります。
でしたので、 上の式は次のようになります。
この式は、 マクローリンの定理を表す式です。
 解析学 へ戻る
解析学 へ戻る