（１） マクローリン展開 の例

　　　
　　　

　　　
　　　

　　　
　　　

　　　
　　　

　　　
　　　

　　　

　　　

　　　
　　　



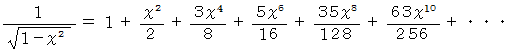
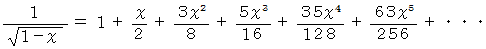
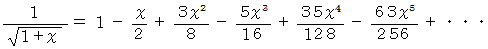
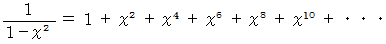
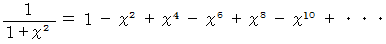
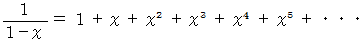
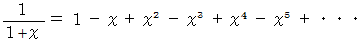
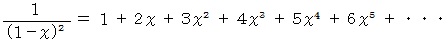
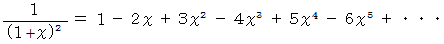
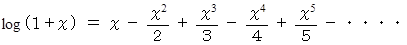
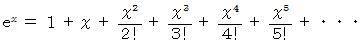
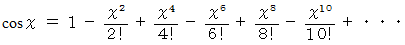
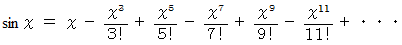
（２） マクローリンの定理 の例

　　　
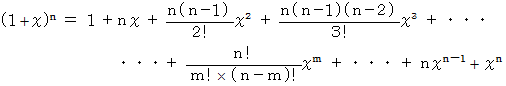
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　この式は、 二項定理 といわれています。

　　　

　　　
　　　
　　　
　　　



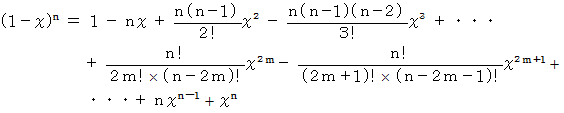
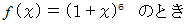
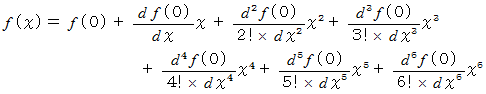
（３） マクローリン展開式には、 x が取れる値の範囲に制限がある。

　
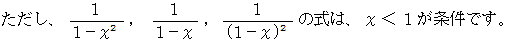
　 なぜならば、 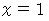のときは、 分母が になりますし、 のときは、 左辺は実数で右辺が無限大になるからです。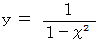

　 のグラフ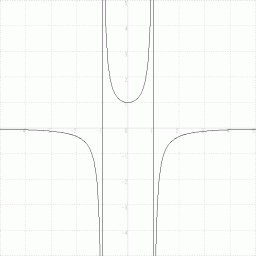
　　　　　


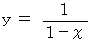　 のグラフ　（ 双曲線 ）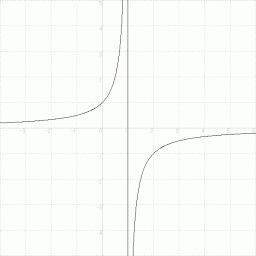
　　　　　


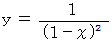　 のグラフ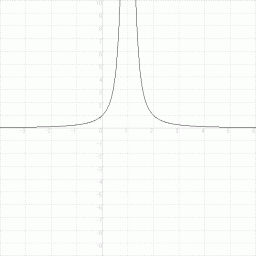
　　　　　


　 マクローリン展開式によって異なりますが、 x が取れる値の範囲に制限があるものが多いです。 十進BASIC のプログラムで確かめてみてください。

プログラムその１
　　

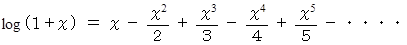
INPUT PROMPT "(-1↑) and (1↓)？":x
LET Q = 0
FOR i=1 TO 2000
　 LET Q = Q - (x^i/i)*(-1)^i
　 PRINT Q
NEXT i
PRINT
PRINT "LOG(1+x) の正解： ";LOG(1+x)
END



プログラムその２　（ 制限のない例 ）
　　

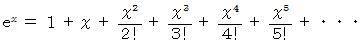
INPUT PROMPT "x？":x
LET Q = 1
PRINT Q
FOR i=2 TO 50
　 LET Q = Q + x^(i-1)/KAIJ(i-)
　 PRINT Q
NEXT i
PRINT
PRINT "ｅのx乗 の正解： ";EXP(x)
END

EXTERNAL FUNCTION KAIJ(n)
LET W=1
FOR i=n TO 1 STEP -1
LET W = W*i
NEXT i
LET KAIJ=W
END FUNCTION



プログラムその３　（ 範囲が狭い例 ）
　　

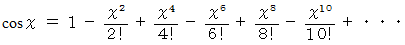
INPUT PROMPT "(-0.5↑) and (0.5↓)？":x
LET Q = 1
PRINT Q
FOR i=2 TO 50
LET Q = Q - x^i/KAIJ(i)*(-1)^i
PRINT Q
NEXT i
PRINT
PRINT "cos(x) の正解： ";COS(x)
END

EXTERNAL FUNCTION KAIJ(n)
LET W=1
FOR i=n TO 1 STEP -1
LET W = W*i
NEXT i
LET KAIJ=W
END FUNCTION