確率 へ戻る（ 問 題 ）
-
魔法の壺と言われる「 ポリアの壺 」の中に、 赤いアメ玉が m 個、 白いアメ玉が n 個 入っています。
第１回目試行 ： この壺から任意に １ 個だけアメ玉を取って食べます。
その後の操作 ： この壺に今食べたアメ玉と同じ色のアメ玉を
１ 個入れます。第２回目試行 ： この壺から任意に １ 個だけアメ玉を取って食べます。
その後の操作 ： この壺に今食べたアメ玉と同じ色のアメ玉を
２ 個入れます。第３回目試行 ： この壺から任意に １ 個だけアメ玉を取って食べます。
以上３回の試行について、 それぞれ赤いアメ玉を食べる確率を求めなさい。
-
第 １ 回目試行 ：
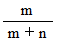
第２回目試行 ：
第１回目試行で赤いアメ玉を食べた場合
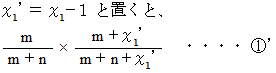
第１回目試行で白いアメ玉を食べた場合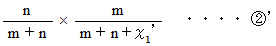
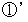
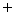
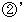より、 答えを求めることができます。 つまり、 次のようになります。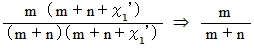
結局、
１ の値は関係ないということ、 第１回目試行と同じ確率であることがわかります。第３回目試行 ：
第２回目試行を第１回目試行と考え、 第３回目試行を第２回目試行と考えると、 第３回目試行は第２回目試行と同じ結果になります。 ということは、 ３回目試行は第１回目試行と同じ結果になります。
（ 以 上 ）
＜ まとめ ＞
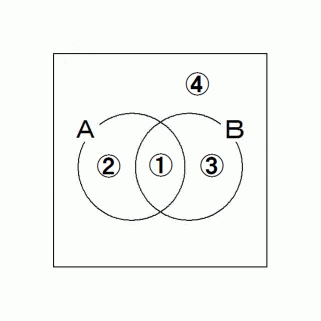
集合Ａ ： 第 k 回目試行で赤いアメ玉を食べる場合
集合Ｂ ： 第 (k+1) 回目試行で赤いアメ玉を食べる場合
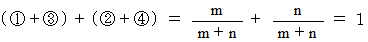
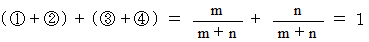
＜ 10 万回試行 のシミュレーション ＞
壺の中に赤または白い玉が全部で 10 個あります。 無作為に１個取り出して、 取り出した玉と同じ色の玉を １ 〜 ４ 個壺の中に入れます。 これを８回繰り返します。
１回目 から８回目 までそれぞれ赤玉を取り出す確率がどれくらいになるかをシミュレートしましょう。