【 問 題 】
-
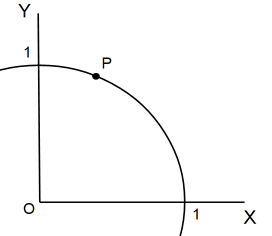
中心が原点にある半径1の円の円周上の 0≦X≦1 かつ 0≦Y≦1 の範囲に点Pがあります。スイッチを押すと1秒後に点Pを無作為にその範囲内の他の場所に移動させるマシーンがあります。移動後の点PのX座標値が root (3) / 2 以上ならば当たりとすることを試行Aとし、移動後の点PのX座標値が 1/2 以上ならば当たりとすることを試行Bとします。最初は試行Aを行い、その後は、前回が当たりだった場合は試行Aを行い、前回がはずれだった場合は試行Bを行います。第1回目と第2回目とが共に当たりになる確率(A)と 第2回目が当たりになる確率(B)と 第3回目が当たりになる確率(C)と 第4回目が当たりになる確率(D)を求めてください。
-
試行A: 点Pの位置ベクトのX軸に対する偏角が 30°以下ならば当たりなので、当たる確率は 1/3 。
試行B: 点Pの位置ベクトのX軸に対する偏角が 60°以下ならば当たりなので、当たる確率は 2/3 。
第1回目も第2回目も当たりになる確率は 1/3 なので、第1回目と第2回目とが共に当たりになる確率(A)は、(1/3)2 =→ 1/9 である。
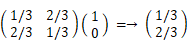
第2回目が当たりになる場合は、第1回目も第2回目も当たりになる場合 と 第1回目がはずれで第2回目が当たりになる場合 の2通りである。後者の確率は、( 1 − 1/3 ) × 2/3 =→ 4/9 だから、第2回目が当たりになる確率(B)は、1/9 + 4/9 =→ 5/9 である。
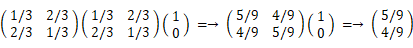
第3回目が当たりになる場合は、第2回目も第3回目も当たりになる場合 と 第2回目がはずれで第3回目が当たりになる場合 の2通りである。前者の確率は、5/9 × 1/3 =→ 5/27 である。後者の確率は、( 1 − 5/9 ) × 2/3 =→ 8/27 である。したがって、第3回目が当たりになる確率(C)は、5/27 + 8/27 =→ 13/27 である。
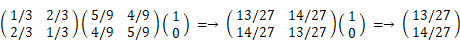
第4回目が当たりになる場合は、第3回目も第4回目も当たりになる場合 と 第3回目がはずれで第4回目が当たりになる場合 の2通りである。前者の確率は、13/27 × 1/3 =→ 13/81 である。後者の確率は、( 1 − 13/27 ) × 2/3 =→ 28/81 である。したがって、第3回目が当たりになる確率(D)は、13/81 + 28/81 =→ 41/81 である。
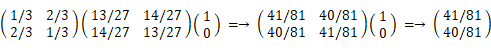
 確率 へ戻る
確率 へ戻る