-
Aの容器には 16 % の濃度の食塩水が 400 g 入っている。
Bの容器には 4 % の濃度の食塩水が 200 g 入っている。
100 g ずつ取り出して入れ替える。
これを n 回 行った直後の、 Aの容器の中の食塩水の濃度を A n % ととし、 Bの容器の中の食塩水の濃度を B n % とする。
A n % と B n % をそれぞれ n を用いて表せ。
( 1992年 自治医大 入試 より )
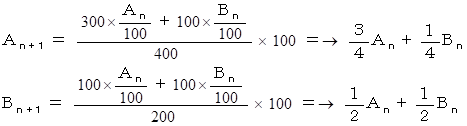
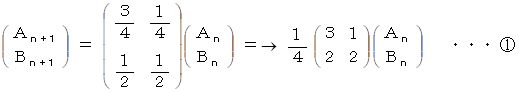


λ = 1 のとき、
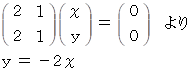
大きさが 1 の固有ベクトルは
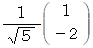
λ = 4 のとき、
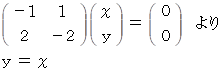
大きさが 1 の固有ベクトルは
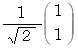
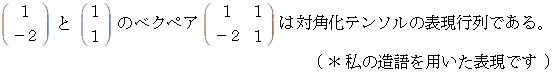
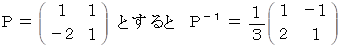
固有空間では、 演算テンソルQの表現行列は次のように座標変換されている。
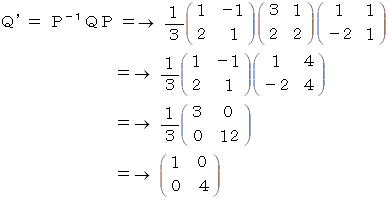
固有空間では、
 の演算は次のように表される。
の演算は次のように表される。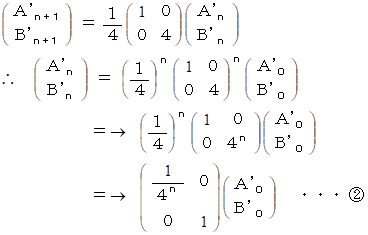
固有空間における
 の演算を元のベクトル空間に座標変換すると、 次のように表される。
の演算を元のベクトル空間に座標変換すると、 次のように表される。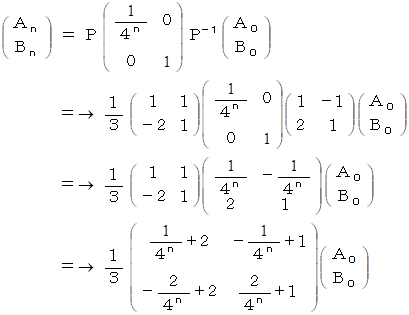
したがって、 答えは次のようになる。
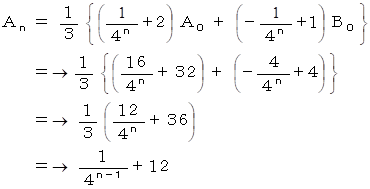
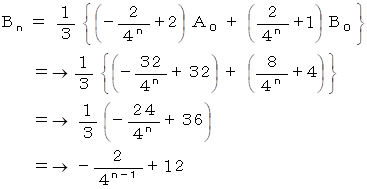
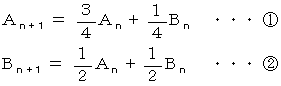
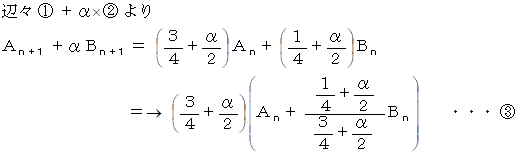

α = −1 のとき、
 は次のようになる。
は次のようになる。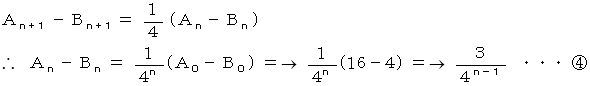
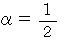 のとき、
のとき、  は次のようになる。
は次のようになる。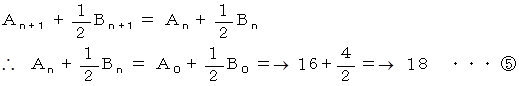

 を
を  に代入して、
に代入して、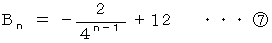
 と
と  が答えになる。
が答えになる。参考: 大学生のための数学 > 確率 > 確率漸化式の問題
 線形代数学 へ戻る
線形代数学 へ戻る