(1) カードの並べ方の場合の数
スペードのカードのみ13枚を用います。 左から右へ順に1枚ずつ表にしてすべてのカードを並べます。 このとき、 一番左の場所に並べるカードの選び方は 13とおり、 左から2番目の場所に並べるカードの選び方は 12とおり、 右から2番目の場所に並べるカードの選び方は 2とおり、 一番右の場所に並べるカードの選び方は 1とおり です。 したがって、 カードの並べ方は全部で 13 ! とおり になります。
この 13 ! とおり を、 十進BASIC の漸化式プログラムを用いて求めてみることにしましょう。 もし、 左から右に向かって3枚だけカードを並べるのであれば、 カードの並べ方は、すべてで 13 × 12 × 11 とおり です。 カードを1枚だけ並べるとき、 カードを2枚並べるとき、 カードを3枚並べるとき、 ・ ・ ・ ・ 、 カードを13枚全部並べるとき、 その並べ方が何とおりあるのかを数列で表すと、 次のようになります。
13 12 × 13 11 × 12 × 13 ・ ・ ・ ・ ・ 1 × 2 × 3 × ・ ・ ・ × 13
したがって、 この数列の漸化式は次のようになります。
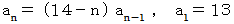
したがって、 次のようなプログラムを作って実行してみましょう。 13 ! を計算した値が出力されます。
(2) 4分音符と2分音符で作るリズム
1小節の時間を
 とします。 4分の
とします。 4分の  拍子のとき、 4分音符の時間は
拍子のとき、 4分音符の時間は 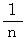 、 2分音符の長さは
、 2分音符の長さは 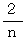 になります。
になります。4分の
 拍子のとき、 1小節を4分音符と2分音符だけで作るとき、 何とおりのリズムができるでしょうか?
拍子のとき、 1小節を4分音符と2分音符だけで作るとき、 何とおりのリズムができるでしょうか?
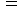
 のとき、
のとき、 
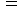
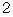 のとき、 ・ ・ ・ ・ と、 1つずつやっていきますと、 それぞれ次のようになります。
のとき、 ・ ・ ・ ・ と、 1つずつやっていきますと、 それぞれ次のようになります。1 2 3 5 8 13 21 ・ ・ ・ ・
この数列をよく観察していると、 次の漸化式が見えてきます。
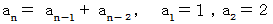
これは、 フィボナッチ数列が1つシフトして、 第
 項目の値 が 第 (
項目の値 が 第 ( 
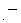
 ) 項目の値になったものです。 どうして、 このようになるのかを考察してみます。
) 項目の値になったものです。 どうして、 このようになるのかを考察してみます。最初に
 個の4分音符で作られた1小節から、 隣り合う4分音符2つを2分音符で置き換えていって、 いろんなリズムに変換させていくという手法をとります。 相撲力士の まわし の さがり を思い浮かべてください。
個の4分音符で作られた1小節から、 隣り合う4分音符2つを2分音符で置き換えていって、 いろんなリズムに変換させていくという手法をとります。 相撲力士の まわし の さがり を思い浮かべてください。
4分の
 拍子のときは、 さがり の数が
拍子のときは、 さがり の数が  個のときに相当し、 最初に
個のときに相当し、 最初に  個の4分音符で作られた1小節から、 隣り合う4分音符2つを2分音符で置き換えることを、 隣どうしのさがりを結びつけることに相当します。 さがり が 1本のとき、 2本のとき、 3本のとき、 ・ ・ ・ ( さがり は左側に次第に増やしていきます ) ・ ・ ・ 、
個の4分音符で作られた1小節から、 隣り合う4分音符2つを2分音符で置き換えることを、 隣どうしのさがりを結びつけることに相当します。 さがり が 1本のとき、 2本のとき、 3本のとき、 ・ ・ ・ ( さがり は左側に次第に増やしていきます ) ・ ・ ・ 、  本のとき の、 さがりの結びつけ方が何とおりあるのかを数列にすると、 次のようになります。
本のとき の、 さがりの結びつけ方が何とおりあるのかを数列にすると、 次のようになります。1 2 3 5 8 13 21 ・ ・ ・ ・
さがり の一番左と左から2番目を結ばない場合は、 さがり の数がそれより1個少ないときの結びつけ方と同じ方法の数あります。 また、 さがり の一番左と左から2番目を結ぶときは、 さがり の数がそれより2個少ないときの結びつけ方と同じ方法の数あります。 「 さがり の一番左と左から2番目を結ばない場合 」 または 「 さがり の一番左と左から2番目を結ぶ場合 」 は全体集合になりますから、 さがり の数がそれより1個少ないときの結びつけ方の数 と さがり の数がそれより2個少ないときの結びつけ方の数 とを加えたものが、 さがり の結びつけ方が全体で何とおりあるのか ( 場合の数 ) を示していることになります。
したがって、 次のようなプログラムを作って実行してみましょう。 上記の数列が出力されます。
 十進
十進