n 個 の物の中から m 個 の物を選ぶ組み合わせの数
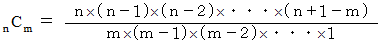
n−1 個 の物の中から m 個 の物を選ぶ組み合わせの数
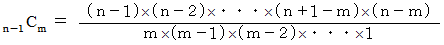
したがって
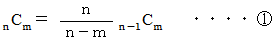
そこで、 次のように置きます。
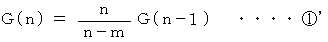
n−1 個 の物の中から m−1 個 の物を選ぶ組み合わせの数
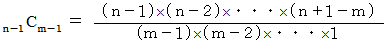
n−2 個 の物の中から m−1 個 の物を選ぶ組み合わせの数
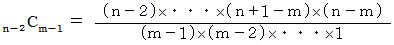
したがって
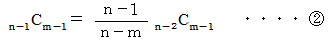
そこで、 次のように置きます。
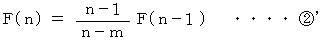

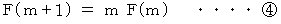
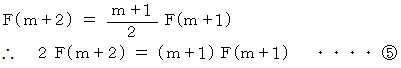
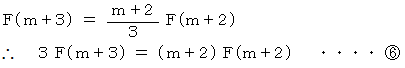
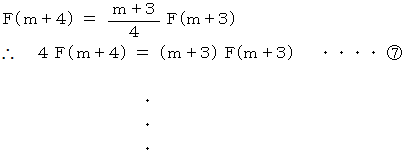
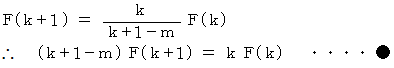
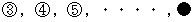 を辺々加えると、
を辺々加えると、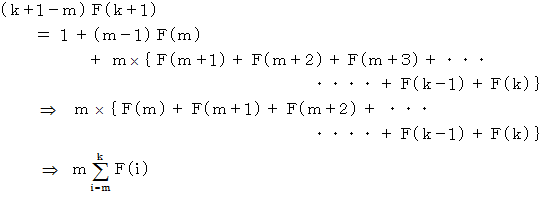
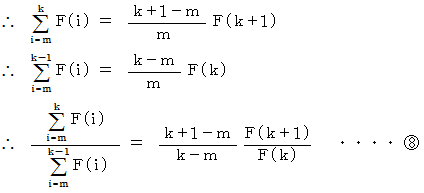
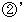 より
より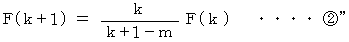
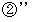 を
を  に代入すると、
に代入すると、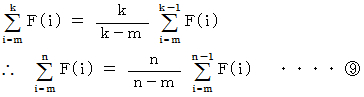
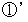 と
と  を比較すると、 次の式が成り立っていることに気づきます。
を比較すると、 次の式が成り立っていることに気づきます。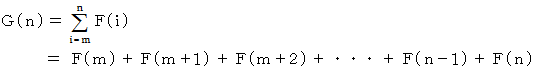
この式は、 一般的に次のような式で表されます。
n+1Cm+1 = mCm + m+1Cm + m+2Cm + ・ ・ ・
・ ・ ・ ・ + n-1Cm + nCm
このことより、 n 個の物の中から m 個の物を選ぶ組み合わせの数は、 m−1 個 の物の中から m−1 個 の物を選ぶ組み合わせの数と、 m 個の物の中から m−1 個 の物を選ぶ組み合わせの数と、 m+1 個 の物の中から m−1 個 の物を選ぶ組み合わせの数と、 ・ ・ ・ ・ ・ ・ ・ ・ ・ と、 n−2 個 の物の中から m−1 個 の物を選ぶ組み合わせの数と、 n−1 個 の物の中から m−1 個 の物を選ぶ組み合わせの数とをすべて加えたものになっていることがわかります。
サイコロを
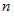 回投げたときの目の数の和が
回投げたときの目の数の和が 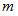 となる場合の数は
となる場合の数は 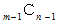 になります。 そこで、十進BASIC で次のようなプログラムを作ることができます。 ( 参考: 確率 > サイコロの目の数の和 )
になります。 そこで、十進BASIC で次のようなプログラムを作ることができます。 ( 参考: 確率 > サイコロの目の数の和 ) 確率 へ戻る
確率 へ戻る