質量 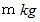の重りの球が、 摩擦なく自由に滑れるレールＧＥがあります。 バネ定数 のバネが自然長のときに、 重りはＧＥの中点Ｏの位置にあります。 このレールを水平に保ったまま点Оを中心に反時計回りに角速度 で等速回転させたところ、 重りが速さ で Ｅ 端に向かって等速直線運動を始めました。 バネが 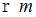伸びたときのバネが縮もうとする力は で、 このときに重りが受ける遠心力もまた です。
このとき、 重りの点Ｏを中心とする回転の速さ 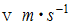（ ） は、 次の式で表されます。
　　　　
重りが移動し始めてからの時間を とすると、 次の式が成り立ちます。
　　　　

　 観察者Ａは と の値をつぶさに観察し記録しました。また、観察者Ｂは と の値をつぶさに観察し記録しました。 そして、 それぞれが次のような関係性を発見しました。
　　　　
そこで２人は相談して、 次のような式を作りました。
　　　　
　 しかし、 これは間違いです。 この式から、 「 は にも にも比例する。」 ということを言うためには、 と が独立であることを示さなければならないのです。 つまり、 を固定しても が自由に変化し、 を固定しても が自由に変化することを示さなければならないのです。 実際は、 次の２つの式が成立しているわけです。
　　　　
これらより、 次の式が成り立ちます。
　　　　
　 この式を見て、「 は の平方根 と の平方根 に比例している。」と考えることも間違いです。 と が独立していない場合、「 は にも にも比例する。」ということを表す式は次の式です。