(1) 正しい考察
-
3つの数の順列の集合A があります。
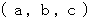
3つの数の順列の集合B があります。
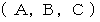
次の写像を考えます。
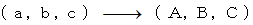
このとき、次の3つの式が成り立っているとします。
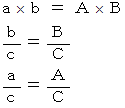
すると、 次のことを言うことができます。
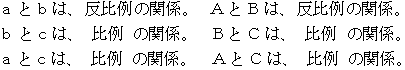
このことを確かめてみます。 次のように置きます。
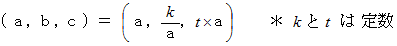
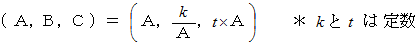
すると、
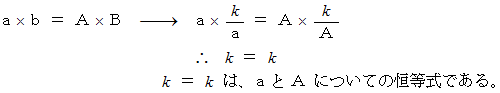
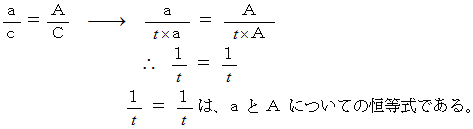
したがって、 次の事柄は成り立っていると言えます。
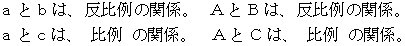
次に、 下のように置きます。

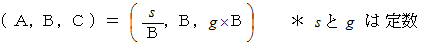
すると、
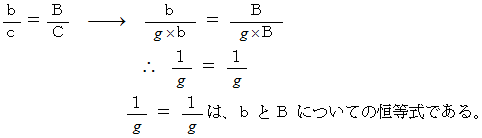
したがって、 次の事柄が成り立っていると言えます。

-
3つの数の順列の集合A があります。
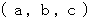
3つの数の順列の集合B があります。
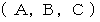
次の写像を考えます。
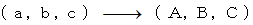
このとき、 次の式が成り立っているとします。
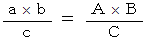
すると、 次のことを言うことができます。

この結論は間違っています。 そのことを明らかにしましょう。 まず、 次のように置きます。

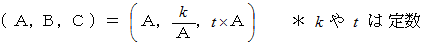
すると、
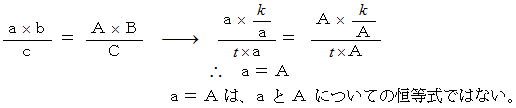
どうもうまくいかないので、今度は次のように置くことにします。
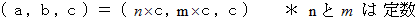

すると、
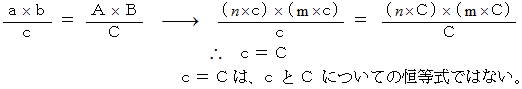
このように、 整合性がありません。 そこで、「 すると、 次のことを言うことができます。」というところを、 次のように書きかえれば正しくなります。

物理学では、 このような例として、 次のような ボイル・シャルルの法則 があります。
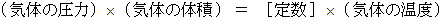
この式は次のようにも書くことができます。
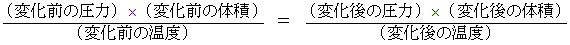
 基礎物理学 へ戻る
基礎物理学 へ戻る