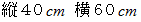の長方形の画用紙を１枚、 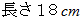の鉛筆を１本用意してください。 鉛筆のちょうど中央部分を 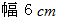に渡って好きな色で塗りつぶしてください。 机の上に画用紙を横にして置いてください。

　 次に、 鉛筆を画用紙の上辺 に沿って置いてください。 これから鉛筆を画用紙の下辺まで滑らせてもらいますが、 下のルールに従ってください。
　　　 　鉛筆は上辺に対して必ず平行にしておくこと。
　　　 　鉛筆を上辺が近づくようには滑らさないこと。
　　　 　鉛筆の中央の色を塗った部分がすべて必ず画用紙上に存在すること。

　 こうして、 鉛筆を画用紙の上辺から下辺に１回滑らせたときの、 鉛筆に色を塗った部分の軌跡に注目してください。 上の条件に従えば、 どんな滑らせ方をしても、 画用紙上の軌跡の面積は必ず 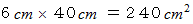になっています。 その理由は、 面積はその範囲の中の平行な線分の長さを積分したものだからです。 また次のようにも考えることができます。

　 まず、 軌跡の両端が曲線になっている部分は、 軌跡の横幅を変えないようにして直線に置き換えます。 そうしても面積が変わらないからです。

　　　　

　 そして、 軌跡の両端の直線が折れ曲がっている高さのところで軌跡を分割します。 すると、 分割された軌跡の形はすべて平行四辺形になっています。（ 長方形も平行四辺形に含まれます。）

　　　　

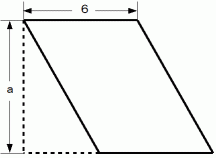
平行四辺形の面積は次のように表されます。
　　　　


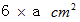
　 次に、 鉛筆の一端が画用紙の中心にくるようにして画用紙の上に置いてください。 今度は、 鉛筆の画用紙の中心部分に存在する端を回転中心にして、 鉛筆を反時計回りに回転させます。 鉛筆をちょうど１回転 させると、 鉛筆の中心点が移動する道のりは 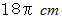になり、 鉛筆を 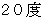回転させると、 鉛筆の中心点が移動する道のりは 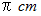になります。 そのときの鉛筆に色を塗った部分の軌跡の面積に注目してください。 鉛筆をちょうど１回転した時の色を塗った部分の軌跡は中抜き円の形をしています。 その面積は 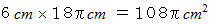になっています。 この中抜き円の面積は次のようにしても求めることができます。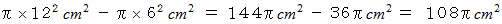
　　　　
鉛筆を 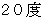回転させたときの色を塗った部分の軌跡の面積の求め方には２つあります。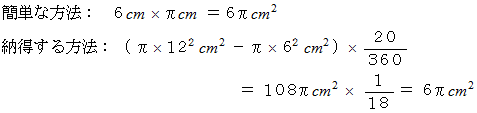
　　　　

　 以上の２つの実験で得られた結論は、 道の総面積を求めるときに役立ちます。 ＮＨＫ高校講座の中で、 秋山仁先生は、 道をいくつかに分割してその半分を反転させてつなぎ合わせることで、 次の公式を視覚的に証明し、
　　　　
その後で、 ＣＤの中にどれだけの情報量を積み込むことができるのかを求めるという、 目から鱗の見事な授業をされています。


　 最後に次の２つの図の道の面積を求める問題を提出しておきます。

　　　　　　　　　　　

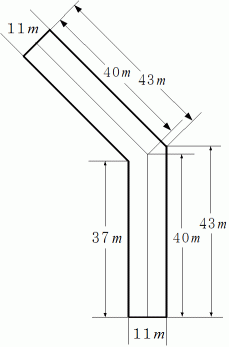
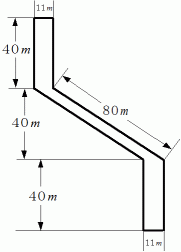
　　　　　　　　　（ 答 え ）　　　左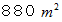図 ：　　　　　　　右図 ：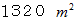　
　 　　　　　　　　　　　　　　　　道幅を変えないための曲がり角の形に注目してください。