道幅が一定の場合、 道の面積は　中央分離帯の長さ × 道幅　で求めることができます。

　 たとえば、 下図のような道であれば、 ３つのパーツに分割し、 真ん中のパーツを反転してつなげると、 赤と青の直線を路肩とし黒の中央分離帯が描かれた直線道路になります。

　　　　　


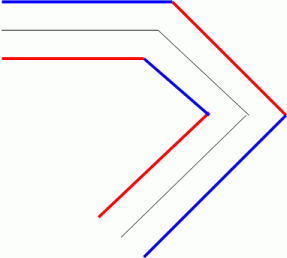
では円形の道ではどうでしょうか？

　　　　　

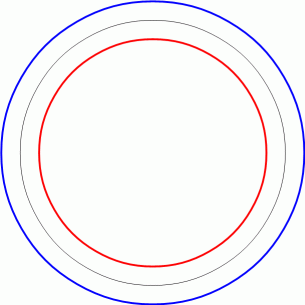
青色の円の半径を ａ 、 赤色の円の半径を ｂ とします。
中央分離帯の長さ × 道幅 は　
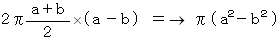
一方、 青色の円の面積から赤色の円の面積を引くと、　

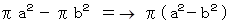
　 したがって、 円形の道でも、 道の面積　＝　中央分離帯の長さ × 道幅　という公式がなりたっていることが判ります。

　 また、 バームクーヘンを均等に１万個に分割し、 隣同士が反転の関係になるようにジグザグに並べ替えると、 長さが π（ ａ ＋ ｂ ） の長い直方体になることも判ります。