個体の物質の 「 内腔 」 とは、 個体の内部に存在する真空または気体または液体で満たされた閉ざされた空間のことです。 「 内腔 」 を形成する曲面は 「 表面 」 ではありません。 物質の 「 表面 」 から 「 内腔 」 に向かって孔を貫通させ、 「 内腔 」 を外界 （ 普通は大気です ） と接するようにすれば、 「 内腔 」 は 「 洞 」 に変わり、 それを形成する曲面は 「 表面 」 となります。

　 「 表 」 と 「 表面 」 とは違います。 「 表 」 とは、 「 サイコロの表と裏 」 や 「 人間性の表と裏 」 や 「 家の表門と裏門 」 のように、 本来、 「 観察者が素直に観察した瞬間に、 見ることのできる物の表面 」 という意味です。 したがって、 私のような不純でこだわりが強い強迫型性格の者は、 「 コインの表裏はいったい誰が決めたのか？ 」 とか 「 野球の表と裏ってなんのこっちゃ？」 と、 ひねくれた 「 よもだ 」 を言います。 ちなみに、 「 表 」 には、 一般的に日当たりの良い側という意味合いもあります。 その例が 「 葉の表と裏 」 です。

　 また、 「 表になっている面 」 と 「 表面 」 とは違います。 「 表になっている面 」 の反対は 「 裏になっている面 」 ですが、 「 表面 」 には反対がありません。 それは、 「 表面 」 が物質の外界と内界の境界曲面だからです。 表面の厚さは限りなくゼロに近いのです。 ならば、 物質の内と外との境界曲面の法線が外界を向いている方を 「 表面 」 とし、 法線が内界を向いている方を 「 内面 」 とすれば良いだろうって？　しかし、 それを言うなら、 「 表面 」 の外界側を 「 表面の外面 」 と言い、 「 表面 」 の内界側を 「 表面の内面 」 と言うべきでしょう。 確かに、 「 表面 」 とは物質の外界と内界の境界曲面で、 外界にも内界にも接しています。


　 それはともかく、 物質の 「 表面 」 は、 ひと繋がりになっています。 たとえば、 ヒトの表面になっている皮膚や粘膜をその下に存在する皮下組織や粘膜下組織から剥離して浮かせると、 それらはすべて繋がっていますので、 その上に接触している点状物質はそれを伝わって体の表面の何処の部分へも移動することができますし、 剥離された表面一塊物質をずらして移動することで、 その上に接触している点状物質は自らが移動しなくとも、 体の表面の何処の部分へも移動することができます。

　 さて、 「 メビウスの輪 」 と 「 クラインの壺 」 という特殊な形状を持った物質あります。 「 メビウスの輪 」 とは、 帯 （ 横幅が比較的長くて奥行きが比較的短い直方体 ） の両側端を相対的に１８０度捻じってから接合した輪のことです。 「 クラインの壺 」 のモデルは、 円柱状の 「 内腔 」 を持つ缶に駆血用ゴム管がぎりぎり通るほどの穴を３つ開けて、 そこに１本の駆血用ゴム管を通し接続固定して作ります。

　　　　

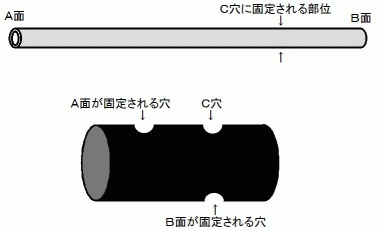
　 これらは、 「 表と裏を判断することが不可能な特殊な物質 」 として紹介されることがありますが、 先ほど申しました 「 表 」 の定義からしますと、 観察の時に、 これらの物質にも表と裏があることになりますので、 表と裏を判断することができないわけではありません。 では、 これらの物質を 「 全ての面が表面になっている特殊な物質 」 として紹介するのはいかがでしょうか？　これも間違いです。 なぜなら、 「 内腔 」 を持たない物質は全ての面が表面になっていますので、 これらが特殊ではないからです。