8-Qeen問題は、 下図のように、 ８×８マスの中に、 縦横斜めが重ならないように８枚のコインを配置する方法を求める問題です。

　　　　　　　　　　　　

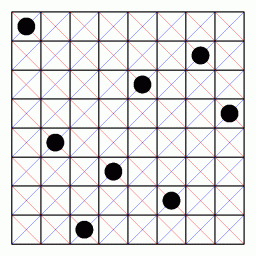
　 マスの行を上から順に １ 〜 ８ 、 マスの列を左から順に １ 〜 ８ とします。 ｎ 行 ｍ 列 のマスの中に ｎ＋ｍ の数字を入れていきますと、 同じ数が斜めに並びます。 また、 ｎ 行 ｍ 列 のマスの中に ｎ−ｍ＋９ の数字を入れていきますと、 同じ数が斜めに並びます。

　　　　

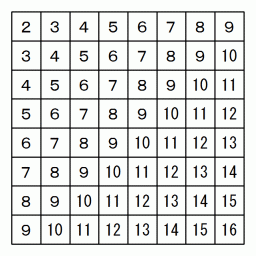
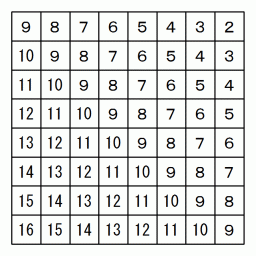
　 このことを応用して、 ８王妃パズルを解くプログラムを作ることができます。
次のプログラムはバックトラック法を利用しています。

　　

　　

　このバックトラック法を利用したプログラムのアルゴリズムの骨子は次のようなものです。
　まず、８個のクィーンを次のように斜めに仮に並べます。
　　　(1,1)　(2,2)　(3,3)　(4,4)　(5,5)　(6,6)　(7,7)　(8,8)
　次に、(1,1) に配置しているクィーンを有効にします。すると、他の７個のクィーン達はすべて置けない所に仮置き状態になります。そこで、２行目のクィーンを１つだけ右に移動させます。このとき、他のクィーンを１つだけ移動させて同じ列に２個以上重ならないようにします。そこで、２行目に仮置かれたクィーンが置いても良い所にあるのかどうかを調べてＯＫならば有効にします。有効にすることができないのならば、さらに２行目のクィーンをもう１つだけ右に移動させます。このときも、他のクィーンを１つだけ移動させて同じ列に２個以上重ならないようにします。そして、２行目に仮置かれたクィーンが置いても良い所にあるのかどうかを調べてＯＫならば有効にします。このような操作を繰り返して行い、行き詰まったら、１つ前の所までバックしてからやり直します。