【 問 題 】

　円周上に無作為に３点を取り、それを頂点として円に内接する三角形を作るとき、その三角形に円の中心が含まれる確率を求めよ。

　【 解 答 】

　まず、円周上に点 P₁ を取る。点 P₁ はどこにとっても確率的には意味が無いので、固定させる。
　次に点 P₂ をとる。点 P₁ と 点 P₂ の円周上の距離は円周の長さの半分以下とする。なぜなら、それ以上にとっても、円を前後反転させると、点 P₁ から 点 P₂ までの円周上の距離は円周の長さの半分以下になるからだ。
　その次に点 P₃ を取るのだが、点 P₁ と 点 P₂ の間の弧と正反対側になる弧の上に点 P₃を取るときにのみ、３点を結んでできる三角形は円の中心を含む。
　ということは、点 P₁ と 点 P₂ を固定したときに、３点を結んでできる三角形に円の中心が含まれる確率は、点 P₁ と 点 P₂ の間の弧の長さを円周の長さで割った値になる。
　問題の答えを得るためには、点 P₁ から 点 P₂ までの円周上の距離を 0 から 円周の長さの半分 まで動かしてその都度の確率を積分したものを、円周の長さで割って平均化すればよいので、答えは次のようになる。
　　　
　　　　　　　　　　　　

　【 別 解 】

円周上に無作為に３点を取り、この３点結んでできる三角形が円の中心を含むとき念願成就とします。
10万回のシミュレーションをします。

　　　　　　　念願成就したのは 　回 でした。



　２次元 x y 座標系の原点Ｏを中心とする円の円周上に無作為に点Ａ、点Ｂ、点Ｃを取ります。それらは x 軸からの偏角が小さい順になっているとします。３つの点を結んでできる三角形ＡＢＣが内部に原点Ｏを含む確率を求めてみましょう。
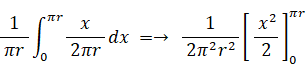
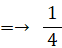
　三角形ＡＢＣが内部に原点Ｏを含むための必要十分条件は、３点がある直径に対してすべて同じ側になっているということがないことです。そのためには、次の３つの条件がすべて満足されなくてはなりません。ただし、ここで用いている角度は、反時計回りを正の方向とする回転ベクトルとしての角度です。
　　　１． ∠ＡＯＢ ＜ ＋180度　（ ３点がある直径に対してすべて同じ側にあっていけません。）
　　　２． ∠ＢＯＣ ＜ ＋180度
　　　３． ∠ＡＯＣ ＞ ＋180度

　最初の点Q₁を取った後２番目の点Q₂を取りますが、そのとき∠Q₁ＯQ₂ の平均は 90 度（ ここでは回転ベクトルとしての角度ではなく、180度以下の交差角度を用いています。）になります。その平均の状態から最後の点Q₃を取ったときに、三角形Q₁Q₂Q₃が内部に原点Ｏを含む確率は次にようにして求めることができます。
　　　90度 ÷ 360度 ＝→ 1/4

プログラムの内容 ：

　【 解 説 】

　この問題は「最初に０〜１の間の実数を無作為に１つ選び、次に０〜２の間の実数を無作為に１つ選んだときに、最初に選んだ数の方が大きくなる確率を求めよ。」という問題と同じです。点Q₃が弧Q₁Q₂上になったときに、点Q₃の正反対側に点Q₄を取ると、三角形Q₁Q₄Q₂は中心を含みます。
　最初に０〜１の間の実数を無作為に１つ選び、次に０〜２の間の実数を無作為に１つ選んだときに、最初に選んだ数の方が大きくなる確率をプログラムシミュレーションにより求めてみましょう。


　　　　　　　10万回のシミュレーションの結果： %