ベクトル解析 へ戻る【 問 題 １ 】
に次の３つの条件が与えられているとき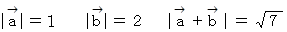
のなす角を求めよ。 のなす角を θ とすると、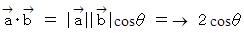 
一方、３つの条件より、
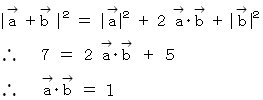
したがって、
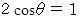
よって、 θ ＝ 60 度
-
x2 ＋ y2 ＋ z2 ＝ １ の球上の点を 点Ｐ（ x， y， z ） とするとき、 x ＋２y ＋３z が最大になる 点Ｐと、x ＋２y ＋３z の最大値を求めよ。
-
座標上に点Ａ（ １，２，３ ）をとり、点Ａ と 点Ｐ の位置ベクトルをそれぞれ次のように表す。
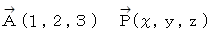
すると、
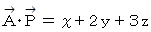
は １ で一定であるので、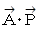 
が最大になるのは、 
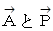の向きが同じになるときである。そこで、 
と置くと、
より、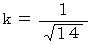
したがって、最大になるのは、
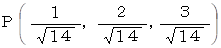
そのときの x ＋２y ＋３z は
になる。