内接遊走歯車
数学と物理学 へ戻る
ばいおりんの日常的物理学文集 へ戻る
2022.06.28_____

　自転公転の相対原理：
　固定回転歯車 Ａ　： 大きさ２　歯車数 24
　固定非回転歯車 Ｂ： 大きさ２　歯車数 24
　固定回転歯車 Ｃ　： 大きさ１　歯車数 12
　遊走回転歯車 Ｄ　： 大きさ１　歯車数 12

　Ａ と Ｃ を外接し、Ｃを反時計回りに１分間に２回自転させると、Ａは反時計回りに１分間に−１回自転する。
　　　Ａからすると、Ｃは反時計回りに１回公転し、かつ、反時計回りに３回自転した。
　　　　　　IJ ＝ −1　 IK ＝ 0　 YJ ＝ 2　 YK ＝ 0

　Ｂ と Ｄ を外接し、Ｄを反時計回りに１分間に３回自転させる。
　　　Ｂからすると、Ｄは反時計回りに１回公転し、かつ、反時計回りに３回自転した。
　　　　　　IJ ＝ 0　 IK ＝ 0　 YJ ＝ 3　 YK ＝ 1

　Ａ と Ｃ を内接し、Ｃを反時計回りに１分間に２回自転させると、Ａは反時計回りに１分間に１回自転する。
　　　Ａからすると、Ｃは反時計回りに−１回公転し、かつ、反時計回りに１回自転した。
　　　　　　IJ ＝ 1　 IK ＝ 0　 YJ ＝ 2　 YK ＝ 0

　Ｂ と Ｄ を内接し、Ｄを反時計回りに１分間に１回自転させる。
　　　Ｂからすると、Ｄは反時計回りに−１回公転し、かつ、反時計回りに１回自転した。
　　　　　　IJ ＝ 0　 IK ＝ 0　 YJ ＝ 1　 YK ＝ −1
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

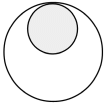
※ コメント：
　完全固定された歯車に接しながら自転し公転する遊走歯車は、２つの接続された固定回転歯車の回転の様子を大きな歯車の立場に立って観察したものとして表現されます。
　完全固定された歯車に接しながら自転し公転する遊走歯車は、その中心が移動した道のりの分だけスリップなしに転がったと考えればいいのです。


　参考： 錯覚と物理学 ＞ 歯車の回転数の錯覚
　　　　 大学生のための物理学 ＞ 剛体力学 ＞ 相対的歯車回転