ロープ や 電線 などの両端を持って垂らしたときにできる曲線は、 カテナリー曲線 と言われます。 重力と張力とのバランスがこのような曲線をつくります。 典型的なカテナリー曲線の方程式として、 次の式が有名です。
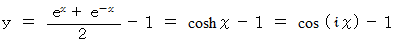
カテナリー曲線を描いている円柱ケーブルの線密度を
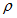 とします。重力加速度を g とします。 カテナリー曲線を描いている円柱ケーブルの両端に作用している張力の水平成分の大きさを
とします。重力加速度を g とします。 カテナリー曲線を描いている円柱ケーブルの両端に作用している張力の水平成分の大きさを  とします。
とします。カテナリー曲線の底点を原点とし、 左右対称になるような座標をとり、 カテナリー曲線の方程式を
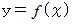 とします。
とします。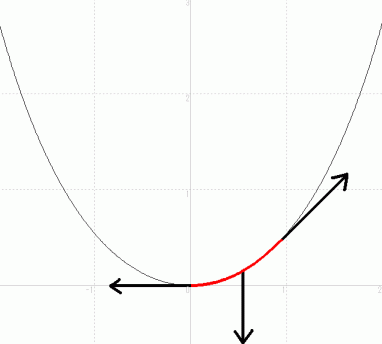
カテナリー曲線を描いている円柱ケーブルの微小部分 ( 微小曲線分 ) の長さを
 とします。
とします。微小曲線分の左端が存在する座標を
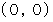 とします。
とします。微小曲線分の右端が存在する座標を
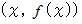 とします。
とします。微小曲線分の右端に働く張力の水平方向からの角度を
 とします。
とします。微小曲線分の左端に働く張力の大きさは
 になります。
になります。微小曲線分の右端に働く張力の水平方向の大きさは
 になります。
になります。微小曲線分の右端に働く張力の鉛直方向の大きさは
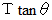 になります。
になります。次の式たちが成り立ちます。
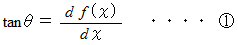
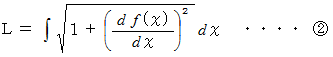
微小部分の鉛直方向の運動方程式 ( 力の吊り合いの式 ) は次のようになります。
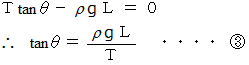
 より、
より、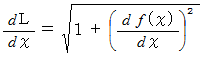
 を代入すると、
を代入すると、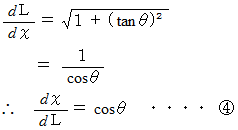
 の両辺を
の両辺を  で微分すると、
で微分すると、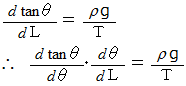
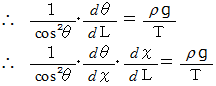
この式に
 を代入して、
を代入して、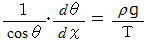
この両辺を
 で積分すると、
で積分すると、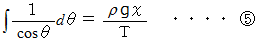
 の左辺は、 Maxima を使って求めると、 次のようになります。
の左辺は、 Maxima を使って求めると、 次のようになります。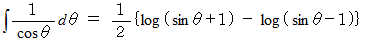
これはさらに、 次のように変形することができます。
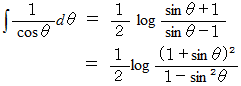
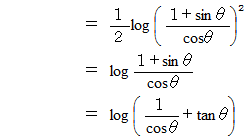
したがって、
 は次のようになります。
は次のようになります。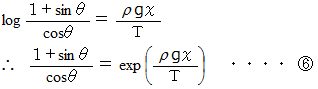
また、
 は次のようにもなります。
は次のようにもなります。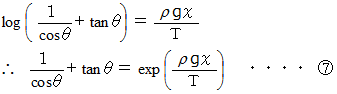
 より
より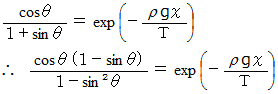
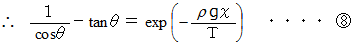
 と
と 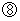 より、
より、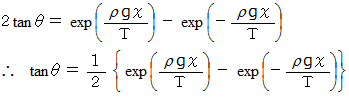
これに
 代入すると、
代入すると、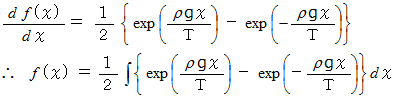
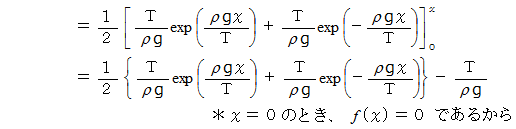
これがカテナリー曲線( 懸垂曲線 )の方程式です。
 材料力学 へ戻る
材料力学 へ戻る