（１） 特殊な場合の２つのベクトルがなす角

　 原点を起点とする大きさが １ の２つのベクトル 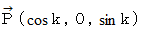（ ｋ は定数 ） と 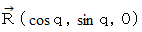（ ｑ は変数 ）があります。 は x z 平面上にあって動かず、 は x y 平面上にあって反時計回りに回転しています。 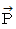と 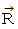とが作る角を とします。　 を ｑ の関数で表してみましょう。

内積の定義と成分表示の式より、 次の式が成り立ちます。
　　　　　
　　　　　　　　　　　　　

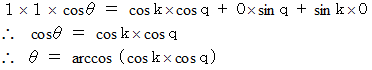
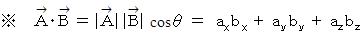
２つのベクトルが作る角の大きさを求めます。
x z 平面上の固定ベクトル（ cos k , 0 , sin k ）の角度 k の値 と
x y 平面上の回転ベクトル（ cos q , sin q , 0 ）の角度 q の値 を
半角数字で入力してから、 決定ボタンを押してください。


　　　 x z 平面上の固定ベクトルの角度 k ：　 度
　　　 x y 平面上の回転ベクトルの角度 q ：　 度
　　　　　　
　　　２つのベクトルが作る角の大きさ ：　 度


k または q が 90度 のとき、 ２つのベクトルのなす角は 90度 になります。

（２） 一般的な場合の２つのベクトルがなす角

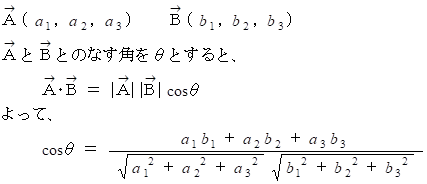
２つのベクトルが作る角の大きさを求めます。
　　　ベクトルＡ ：　
　　　ベクトルＢ ：　
　　　　　　
　　　２つのベクトルが作る角の大きさ ：　 度