互いに実力の等しい野球チーム Ａ と Ｂ があります。 これから Ａチーム と Ｂチーム は何度も対戦し （ 引き分けはないことにします ）、 先に４勝したチームが今年の王者であるとします。
　 ４勝０敗パターン、 ４勝 １ 敗パターン、 ４勝２敗パターン、 ４勝３敗パターン、 と４とおりの優勝パターンがありますが、 それぞれにそうなる確率を求めてみましょう。

　 Ａチームが優勝するときの確率を求め、 それを２倍すれば答えになります。
Ａチームの４勝０敗優勝になるときは、 必ず優勝が決まる前日はＡチームの３勝０敗になっており、
Ａチームの４勝 １ 敗優勝になるときは、 必ず優勝が決まる前日はＡチームの３勝 １ 敗になっており、
Ａチームの４勝２敗優勝になるときは、 必ず優勝が決まる前日はＡチームの３勝２敗になっており、
Ａチームの４勝３敗優勝になるときは、 必ず優勝が決まる前日はＡチームの３勝３敗になっています。

　 したがって、
　　　　　
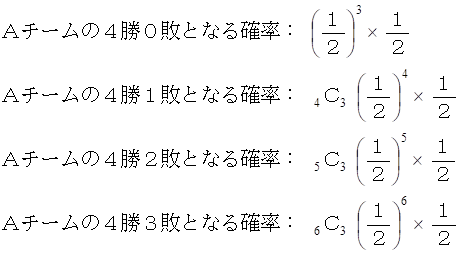
　 したがって、
　　　　　


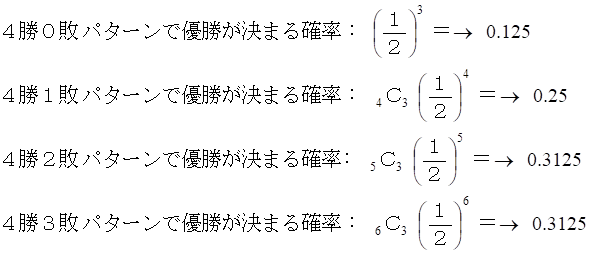
シミュレーションしてみます。（ 10万回試行 ）

　　　　　　

プログラムの内容 ：