（１） サイコロを10 回振ったときに、 1 の目が３回だけ出る確率を求めよ

　「 第 結果席 」には、 回目に出た目の数が入るとします。

　 10 回サイコロを振った時に、 最初の３回続けて 1 の目が出て、 残りはすべて 1 以外の目が出る確率は、 次のようになります。
　　　　
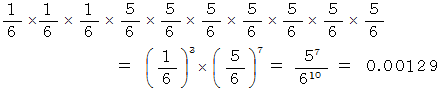
　 10 回サイコロを振った時に、「 第１結果席 」と「 第２結果席 」と「 第４結果席 」に 1 が入り、その他の結果席には 1 以外の数が入る確率は、 次のようになります。
　　　　
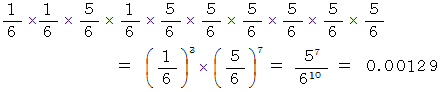
　 10 回サイコロを振った時に、「 第３結果席 」と「 第７結果席 」と「 第９結果席 」に 1 が入り、 その他の結果席には 1 以外の数が入る確率は、 次のようになります。
　　　　
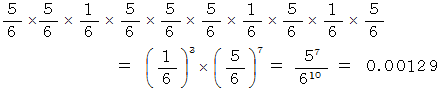
　 このように考えていくと、
　 「 結果席の組み合わせ 」が全部で何とおりあるのかを調べて、 それを 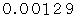にかければ、 答えを導くことができることに気づきます。

　 ではまず、「 第１表彰台 」、「 第２表彰台 」、「 第３表彰台 」に上がる「 すべての結果席 」の「 順列の数（ 単位： とおり ）」を求めます。
　　　　
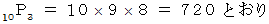
　 次に、「 第１倉庫 」、「 第２倉庫 」、「 第３倉庫 」に入る「 ３つの表彰台 」 の「 順列の数 （ 単位： とおり ）」を求めます。
　　　　　
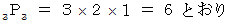
　 すると、「 ３台収納倉庫 」に入る「 すべての結果席 」の「 組み合わせの数 （ 単位： とおり ）」は次のようになります。
　　　　

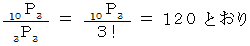
したがって、求める確率は、次のようになります。
　　　　

（２） 二項分布

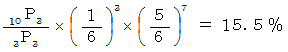
　一般に、 １ 回の期待確率が 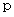の独立な試行を 回 行ったときに、 回だけ期待どおりになる確率は、 次のように表されます。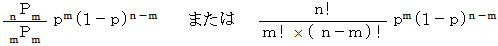
　　　　
　　　　　　　　　

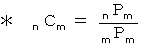
　期待どおりになる回数 （ ） を 軸に、 回だけ期待どおりになる確率を 軸にして、 プロットし隣どうしを線で結びますと、 を頂点とする左右対称の山型のグラフになります。 この二項分布は確率分布であり、 次の式が成り立ちます。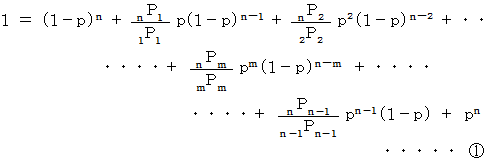

　　　　

　 この二項分布の名前は、 二項定理に由来します。

二項定理 ：
　　　
　　　
　　　　　　
　　　　　　

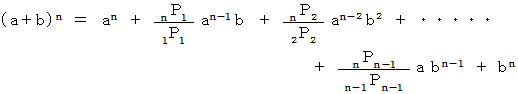
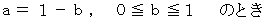
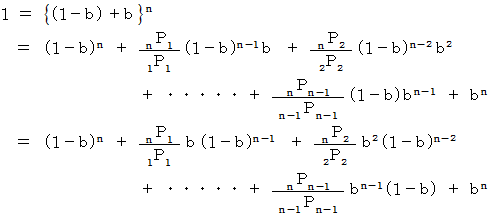
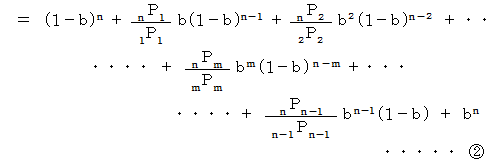
　 と は同じ形をしています。

（３） 組み合わせの数の分布

　 Ａ君とＢ君がジャンケンを10 回します。 Ａ君が勝つ回数ごとの確率は次のようになります。

　　　
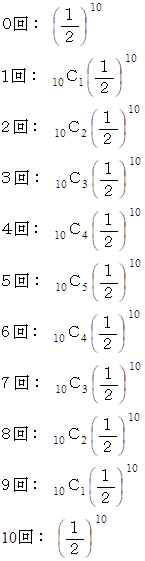
　 以上より、 独立試行の確率が ２分の １ の場合、「 独立試行の反復による頻度の確率 」の分布は、上記の 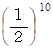を消去して、 組み合わせの数の分布になっていることがわかります。

　※ 参照： 大学生のための数学 ＞ JavaScript ＞ JavaScript＿シミュレーション ＞ 二項分布確率