十進大きさの異なる相似形をした皿が ｎ枚 あります。 皿の直径は等比数列になっています。 それらは全て、 地点１ に重ね置かれています。 上に行くほど小さな皿になるようにして。 皿を置くことのできる地点には 地点１ の他に 地点２ と 地点３ があります。 そこで、 他の皿に触れることなく１枚ずつ皿を移動させて、 同じ地点に置かれた皿は必ず上に行くほど小さくなるように重ねていき、 地点１ に重ね置かれていた皿をすべて 地点２ に移動させるには、 最小で何回皿を移動させなければならないでしょうか。
例えば２皿の場合は、 上の皿を 地点３ に移動させ、 次に下の皿を 地点２ に移動させ、 最後に上の皿を 地点２ に移動させるという、 最小３回になります。 ３皿の場合は、 一番小さな皿を 地点２ に移動させ、 次に真ん中の皿を 地点３ に移動させ、 その次に一番小さな皿を 地点３ に移動させ、 その次に一番大きな皿を 地点２ に移動させ、 その次に一番小さな皿を 地点１ に移動させ、 その次に真ん中の皿を 地点２ に移動させ、 最後に一番小さな皿を 地点２ に移動させるという、 最小７回になります。 一般的な答えは
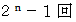なのですが、 今日お話ししたいことは、 この答えの導き方ではなく、 十進BASIC のプログラムがこんなにも短いものであるのかということです。 それは再帰関数を利用したプログラムです。 しかし、 プログラムを見ただけではそのアルゴリズムがなかなか理解できません。 そこで、 今日はそれを解説したいと思うのです。三重大教育学部の奥村晴彦教授は、 著書 「 Ｃ言語最新アルゴリズム辞典 」 に記載されているソースコードをネット上で公開されていますが、 その一部を 山中和義 / 電脳遊戯団 さんが十進BASIC に翻訳されてネット上に公開されています。 そこに 「 ハノイの塔 」 を解くプログラムがあります。 それを掲載させていただきます。
10 SUB movedisk(n,a,b)
20 IF n>1 THEN CALL movedisk(n-1,a,6-a-b)
30 PRINT " ";n;"番目に小さな皿を 地点";a;"から 地点";b;"に移す。"
40 IF n>1 THEN CALL movedisk(n-1,6-a-b,b)
50 END SUB
60 INPUT PROMPT "皿の枚数は？ ":n
70 PRINT n;"枚の皿を 地点１ から 地点２ に移す方法は、次の";2^n-1;"手です。"
80 CALL movedisk(n,1,2)
90 END
60 〜 90 がプログラムの本幹です。 10 〜 50 が再帰関数です。 関数の中で自分自身を呼び出すのが再帰関数です。 このプログラムを実行して、 皿の枚数に４を指定すると、 次のように出力されます。 ただし、 右側の番号は出ませんし、 行のズレもありません。
1 番目に小さな皿を 地点 1 から 地点 3 に移す。 （１）
2 番目に小さな皿を 地点 1 から 地点 2 に移す。 （２）
1 番目に小さな皿を 地点 3 から 地点 2 に移す。 （３）
3 番目に小さな皿を 地点 1 から 地点 3 に移す。 （４）
1 番目に小さな皿を 地点 2 から 地点 1 に移す。 （５）
2 番目に小さな皿を 地点 2 から 地点 3 に移す。 （６）
1 番目に小さな皿を 地点 1 から 地点 3 に移す。 （７）
4 番目に小さな皿を 地点 1 から 地点 2 に移す。 （８）
1 番目に小さな皿を 地点 3 から 地点 2 に移す。 （９）
2 番目に小さな皿を 地点 3 から 地点 1 に移す。 （10）
1 番目に小さな皿を 地点 2 から 地点 1 に移す。 （11）
3 番目に小さな皿を 地点 3 から 地点 2 に移す。 （12）
1 番目に小さな皿を 地点 1 から 地点 3 に移す。 （13）
2 番目に小さな皿を 地点 1 から 地点 2 に移す。 （14）
1 番目に小さな皿を 地点 3 から 地点 2 に移す。 （15）
再帰関数は、 フルクタルと同じで、 内部に入っても先ほどの次元と同じ構造が繰り返されます。 では、 皿４枚の例で、 この再帰関数の内容を見ていくことにしましょう。
movedisk(n,a,b) は、 地点 a にある ｎ枚 に重ねられた皿たちを 地点 b に移すという操作をします。 最初はｎ以外の数文字には捕らわれないようにしてください。 この再帰関数は２回も自分自身を呼び出していますので、 気管が細くなるにつれて２つずつに枝分かれしているような構造になっています。 言うならば、 この再帰関数は再帰分岐関数なのです。 再帰関数の内容を理解するためには、 それを内側から眺めるのではなく外側から眺めることが大切です。 つまり、 枝分かれしていく大本から眺めることが大切です。 まず、 ４枚の皿を、 最大の皿 と 最大の皿以外の皿の塊 の２つの塊として見てください。 再帰関数を外側から眺めたときに、 30 は最大の皿 （ ４番目に小さな皿 ） を 地点１ から 地点２ に移すことを意味します（８）。 ということは、 20 は最大の皿以外の皿の塊をばらしながら最終的に 地点１ から 地点３ にすべて移しているということです（１〜７）。 最大の皿が 地点１ から 地点２ に移動する直前には、 地点３ において最大の皿以外の皿の塊ができています。 40 は最大の皿以外の皿の塊をばらしながら最終的に 地点３ から 地点２ にすべて移しているということになります（９〜１５）。 こうして、 目的が達成されると同時に、 再帰関数の皮が１皮むけてその中が少し見えてきます。 １皮むけた再帰関数は、 ３番目に小さな皿までの３枚の皿を取り扱う次元になっています。 そしてそれは、 最大の皿が 地点１ から 地点２ に移動する前と後との２層になっています。
そこで、 まず、 最大の皿が 地点１ から 地点２ に移動する前の１皮むけた再帰関数の前層から見ていくことにしましょう。 １皮むけた前層の再帰関数を外側から眺めたときに、 ３番目に小さな皿 と それより小さな皿たちの塊 の２つの塊として見てください。 30 は３番目に小さな皿を 地点１ から 地点３ に移すことを意味します（４）。 とういことは、 20 は３番目に小さな皿以外の皿の塊をばらしながら最終的に 地点１ から 地点２ にすべて移しているということであり（１〜３）、 40 は３番目に小さな皿以外の皿の塊をばらしながら最終的に 地点２ から 地点３ にすべて移している（５〜７）ということになります。 こうして、 １皮むけた前層の再帰関数の皮の２皮目がむけました。 すると、 ２番目に小さな皿 と 最小の皿 の２枚だけが見えてきます。 ２皮むけた前層の再帰関数を外側から眺めたときに、 30 は２番目に小さな皿を 地点１ から 地点２ に移すことを意味します（２）。 とういことは、 20 は最小の皿を 地点１ から 地点３ に移すこと（１）を意味するということであり、 40 は最小の皿を 地点３ から 地点２ に移すこと（３）を意味するということになります。 こうして、 前層の再帰関数の皮がすべてむけました。
次は、 最大の皿が 地点１ から 地点２ に移動した後の１皮むけた再帰関数の後層を見ていきましょう。 １皮むけた後層の再帰関数を外側から眺めたときに、 ３番目に小さな皿 と それより小さな皿たちの塊 の２つの塊として見てください。 30 は３番目に小さな皿を 地点３ から 地点２ に移すことを意味します（12）。 とういことは、 20 は３番目に小さな皿以外の皿の塊をばらしながら結局は 地点３ から 地点１ に移している（９〜11）ということであり、 40 は３番目に小さな皿以外の皿の塊をばらしながら結局は 地点１ から 地点２ に移している（13〜15）ということになります。 こうして、 １皮むけた後層の再帰関数の皮の２皮目がむけました。 すると、 ２番目に小さな皿 と 最小の皿 の２枚だけが見えてきます。 ２皮むけた後層の再帰関数を外側から眺めたときに、 30 は２番目に小さな皿を 地点１ から 地点２ に移すことを意味します。 とういことは、 20 は最小の皿を 地点１ から 地点３ に移すこと（13）を意味するということであり、 40 は最小の皿を 地点３ から 地点２ に移すこと（14）を意味するということになります。 こうして、 後半の再帰関数の皮が３皮ともむけ、 すべてが終了しました。
今は皿が４枚の場合でしたが、 皿の枚数が多いときは、 この再帰関数を外側から眺めながら１つずつ皮をむいて次元を変更させていくたびに層が２乗ずつ厚くなっていくので、 相当な時間を要します。 また、 私たちがこの再帰関数の内容を観察した順番は、 ノートの左から右に向かって２つずつ分岐していくイメージであるのに対して、 このプログラムの結果の打ち出し方は、 その逆で、 ノートの右から左に向かって２つずつ分岐していくイメージになっています。
では、 movedisk(n,a,b) の中の数がどのように変化していくのかを見ていきましょう。 ４枚の皿で考えます。 もちろん外側から内側へと向かって見ていきます。
前層の再帰関数は movedisk(n,a,b)
movedisk(n-1,a,6-a-b) と変化します。後層の再帰関数は movedisk(n,a,b)
movedisk(n-1,6-a-b,b) と変化します。前層の再帰関数は、 移しかえる前の地点は一定で、 移し換える地点が次元が変化する
たびに交互に変化します。
後層の再帰関数は、 移し換える地点は一定で、 移し換える前の地点が次元が変化する
たびに交互に変化します。
(1,1,3) ・・・・（１）
(2,1,2)
(1,3,2) ・・・・（３）
(3,1,3)
(1,2,1) ・・・・（５）
(2,2,3)
(1,1,3) ・・・・（７）
(4,1,2)
(1,3,2) ・・・・（９）
(2,3,1)
(1,2,1) ・・・・（11）
(3,3,2)
(1,1,3) ・・・・（13）
(2,1,2)
(1,3,2) ・・・・（15）
＜ コピペ用の小窓 ＞