十進（１） 頭の準備体操
答えは、
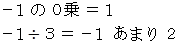
（２） ハノイの塔の問題の解法の法則
大きさの異なる相似形をした皿が４枚 あります。 皿の直径は等比数列になっています。 それらは全て、 地点Ａ に重ね置かれています。 上に行くほど小さな皿になるようにして。 皿を置くことのできる地点には 地点Ａ の他に 地点Ｂ と 地点Ｃ があります。 そこで、 他の皿に触れることなく１枚ずつ皿を移動させて、 同じ地点に置かれた皿は必ず上に行くほど小さくなるように重ねていき、 地点Ａ に重ね置かれていた皿をすべて 地点Ｂ に移動させるには、 最小で
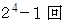皿を移動させる必要があります。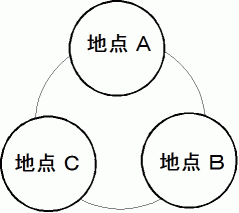
ハノイの塔の手法は次の２つの法則に則っています。
第１法則 ： 回転方向の法則
第１皿 （ 最も小さな皿） と 第３皿 は １地点ずつ反時計回りに移動させ、
第２皿 と 第４皿 は１地点ずつ時計回りに移動させる。
第２法則 ： 移動順の逆分岐の法則
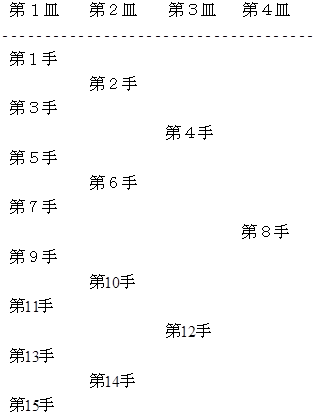
第２法則は、 次のような手法に置き換えることができます。
２進数 逆並べ 非最左１消
100011000100020010010001003001111001000401000010001050101101010006011001100100701111110100081000000100019100110011000101010010101001110111101100012110000110010131101101110001411100111010015111111111000この２つの法則を利用することにより、 ハノイの塔の答えを記述するプログラムを作ることができます。