( 問題 1 )
-
あなたは今、 コインを100枚持っています。 次のゲームを100回した直後にあなたが100枚以上のコインを手にしている確率はおよそ何%でしょうか?
( ゲームの内容 )
1〜50までの自然数のうち1つの数字を言います。
ディーラーが1〜50までのカードの中から無作為に 1 枚を選びます。
ディーラーが選んだカードが自分が言った数字と一致したときは、 ディーラーからコイン
を50枚もらえます。
それ以外の時は、 勝負に負けたことになり、 ディーラーからコインを1枚を取り上げられ
ます。
-
このゲーム1回のコイン獲得数の期待値は、次のようになっています。

したがって、 このゲームは、 何度も繰り返して行えば、 損するよりも得する可能性の方が高いということです。 ただし、 ゲーム1回ごとについては、 コインが増える可能性よりもコインが減る可能性の方が圧倒的に高いのです。 そして、 平均でも最初から34回は負け続けます。 なぜなら、 負け続ける確率が次のようになっているからです。

この種のゲームは負けても負けても辛抱強く続けることです。 途中で投げ出すと、 ディーラーの思う壺に入ります。 かといって、 もし期待値がマイナスの場合は、 負け始めたら直ぐにゲームを引き上げないと、 ディーラーの餌食になってしまいます。
さて、 解答に参りましょう。 このゲームを100回したときに、 コインが100枚以上になっているための必要十分条件は2回以上勝っておくことです。 その確率は次のようにして求めることができます。
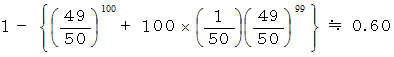
したがって、 答えは、 およそ60%です。
ちなみに、 このゲームを100回したときのコイン獲得数の期待値は、 次のようになります。

したがって、 100回ゲームをした直後は平均102枚のコインを持っていることになります。 ただし13%の確率で、 1枚もコインをもっていないケースが出現します。
シミュレーション :
( 問題 2 )
-
あなたは今、 コインを100枚持っています。 次のゲームを100回した直後にあなたが100枚以上のコインを手にしている確率はおよそ何%でしょうか?
( ゲームの内容 )
まず、 ディーラーからコインを1枚取り上げられます。
1 〜 9 までの自然数のうち1つの数字を言います。
ディーラーが 1 〜 50 までのカードの中から任意に1枚を選びます。
ディーラーが選んだカードが自分が言った数字と一致したときは、 ディーラーからコイン
を50枚もらえます。
それ以外の時は、 勝負に負けたことになり、 なにももらえません。
-
このゲーム1回のコイン獲得数の期待値は、 次のようになっています。
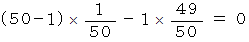
したがって、 このゲームは、 何度も繰り返して行えば、 損得の可能性が半々です。 ただし、 ゲーム1回ごとについては、 コインが増える可能性よりもコインが減る可能性の方が圧倒的に高いのです。 そして、 平均でも最初から34回は負け続けます。 この種のゲームは負けても負けても辛抱強く続けることです。 途中で投げ出すと損をします。 ただし、 勝って元々持っていたコインよりも随分多くなった場合は直ぐにゲームから引き上げることをお勧めします。 ディーラー泣かせの引き際上手です。
このゲームを100回したときに、 コインが100枚以上になっているための必要十分条件は2回以上勝っておくことです。 その確率は次のようにして求めることができます。
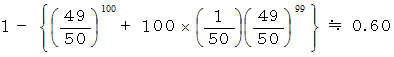
したがって、 答えは、 およそ60%です。 先ほどの問題の答えと同じです。
ちなみに、 このゲームを100回したときのコイン獲得数の期待値は、 次のようになります。
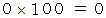
したがって、 100回ゲームをした直後は平均100枚のコインを持っていることになります。 ただし13%の確率で、 1枚もコインをもっていないケースが出現します。 ちょうど50枚コインを持っているケースが出現する確率と、 ちょうど100枚コインを持っているケースが出現する確率と、 ちょうど150枚コインを持っているケースが出現する確率と、 ちょうど200枚コインを持っているケースが出現する確率は、 それぞれ次のようになります。

シミュレーション :
プログラムの内容 :
 確率 へ戻る
確率 へ戻る