(1) 応力
-
空気を閉じ込めた注射器の内筒を押したり引いたりしますと、 中の空気の圧力は一様に変化します。 つまり、 空間的には等しくて、 時間的には大きくなったり小さくなったりします。 金属のような剛体に近い一様な物質 や ゴムのような軟体の物質 を、 圧縮しようとしたり伸展させようとしたりしたときにも、 物質の内部の圧力が一様に変化します。
円柱物質の両端に向きが反対で大きさが
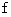 の2つの力が作用しているとき、 その物質の内部の任意の点には、 力は作用していません。 しかし、 それは、 2つの反対向きの大きさの等しい力に分解されます。
の2つの力が作用しているとき、 その物質の内部の任意の点には、 力は作用していません。 しかし、 それは、 2つの反対向きの大きさの等しい力に分解されます。数学であれば、
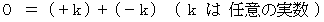 ですが、
ですが、物理学ですから、
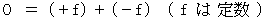 です。
です。このとき、「 物質の内部には応力が作用している。」と言います。「 応力 」は圧力のようなもので、 一種のストレスです。 同じ大きさの2つの力であっても、「 圧縮するように作用する力たち 」 と 「 伸展させるように作用する力たち 」の区別をしなければなりません。 そこで、 前者にはマイナスの記号を付けて「 圧縮応力 」ということにし、 後者にはプラスの記号を付けて「 引張応力 」ということにしましょう。 これらの縦軸方向の応力はまとめて「 垂直応力 」と言われ、 その大きさは次のように表されます。

また、 もう1つ区別しなければならないケースがあります。 それは、 円柱の両端に先ほどの力と垂直な方向に向きが反対で大きさが
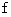 の2つの力が作用しているときに、 物質の内部で打ち消し合っている2つの力のペアです。 これらは、 円柱物質を横方向に引き裂こうとします。 これは「 剪断応力 」といわれます。
の2つの力が作用しているときに、 物質の内部で打ち消し合っている2つの力のペアです。 これらは、 円柱物質を横方向に引き裂こうとします。 これは「 剪断応力 」といわれます。これらの応力は、 円柱の縦中心軸に対して垂直な断面( 円柱の横断面 ) の微小部分ごとに存在していますので、 単位は
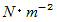 で、 圧力の単位と同じです。
で、 圧力の単位と同じです。-
円柱物質の両端に作用して応力を生む力のペアには、 次の5組があります。
- 「 圧縮力 」:
- 円柱の両底面に垂直で逆向きの力であり、 押しつぶそうとする方向である。
一様な「 圧縮応力 」を生む。
- 「 引張力 」:
- 円柱の両底面に垂直で逆向きの力であり、 引きちぎろうとする方向である。
一様な「 引張応力 」を生む。
- 「 ずり力 」:
- 円柱の両底面に平行で逆向きの力である。
「 ずり力 」の方向に垂直な円柱の縦軸中心を含む縦断面上の点を最大とし、 それから離れるに従って次第に0に近づいていく「 剪断応力 」を生む。
- 「 屈曲力 」:
- 円柱の両底面に平行で同じ向きの力である。
「 屈曲力 」の方向に垂直な円柱の縦中心軸を含む縦断面上の点には応力を生まず、 曲がりの腹側には「 圧縮応力 」を、 曲がりの背側には「 引張応力 」を生む。 それらの「 垂直応力 」の大きさは、 腹側中心表面 あるいは 背側中心表面 に近づくほど大きくなる。
曲がりの方向に垂直な円柱の縦中心軸を含む縦断面からの距離を
 、 円柱の長さを
、 円柱の長さを 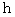 、円柱の底面の直径を
、円柱の底面の直径を 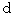 、 両端に同じ向きに作用する屈曲力の大きさを
、 両端に同じ向きに作用する屈曲力の大きさを 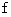 とすると、 次のようになる。
とすると、 次のようになる。
- 「 捻転力 」:
- 円柱の縦中心軸上の点には応力を生まず、 それから周辺にいくほど大きくなる「 剪断応力 」を生む。 その「 剪断応力 」は、 円柱の横断面上にあって円柱の縦中心軸上の点と結ぶ直線に対して垂直な方向であり、 捻転の度合いを僅かに強くしたときに変位する方向である。
縦中心軸からの距離を
 、 円柱の底面の直径を
、 円柱の底面の直径を 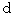 、 両端に反対向きに作用する捻転力のモーメントの大きさを
、 両端に反対向きに作用する捻転力のモーメントの大きさを  とすると、 次のようになる。
とすると、 次のようになる。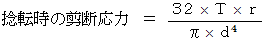
-
「 応力 」を円柱の縦中心軸と垂直な断面( 円柱の横断面 ) の範囲で積分したものを「 断面力 」と言います。「 断面力 」は次の4つに分類することができます。
- 軸力 :
- 「 圧縮力 」や「 引張力 」が生み出す物体内部の力
「 垂直応力 」を円柱の縦中心軸と垂直な断面( 円柱の横断面 ) の範囲で積分したものである。
垂直応力が
 のときは、 軸力は
のときは、 軸力は 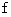 になる。
になる。- 剪断力 :
- 「 ずり力 」が生み出す物体内部の力
「 剪定応力 」を円柱の縦中心軸と垂直な断面( 円柱の横断面 ) の範囲で積分したものである。
- 曲げモーメント :
- 「 屈曲力 」が生み出す物体内部の力
垂直応力に縦中心軸からの距離をかけた「 垂直応力モーメント 」を、 縦中心軸と垂直な断面( 円柱の横断面 ) の範囲で積分したものである。(「 圧縮応力 」と「 引張応力 」は互いに逆向きである。)
- 捻じりモーメント :
- 「 捻転力 」が生み出す物体内部の力
円柱の縦中心軸と垂直な断面( 円柱の横断面 ) を縦中心軸を中心に回転させようとする力
剪断応力に縦中心軸からの距離をかけた「 剪断応力モーメント 」を、 円柱の横断面の範囲で積分したものである。
-
3次元直交座標系の \(y z\) 平面 の第1象限、 \(z x\) 平面 の第1象限、 \(x y\) 平面 の第1象限 にそれぞれべたっと接触し、頂点の1つが原点に存在する微小立方体があります。立方体の相対する面に重心を通る直線の向きに逆向きで大きさが等しい力を加えると、立方体は移動も回転もせずに、圧縮・伸展・剪断されます。この応力を記述するのが次の応力テンソルです。
\[ \begin{flalign}
\ \ \ \ \ \ \begin{pmatrix} \ S_{xx} & S_{xy} & S_{xz}\ \\ \ S_{yx} & S_{yy} & S_{yz}\ \\ \ S_{zx} & S_{zy} & S_{zz}\ \end{pmatrix}&&
\end{flalign} \]
1行目は \(x=0\) の \(yz\) 平面上にある立方体の面の対面に作用している力を表します。
\(S_{xx}\) は \(x\) 軸方向の力の大きさを表します。
\(S_{xy}\) は \(y\) 軸方向の力の大きさを表します。
\(S_{xz}\) は \(z\) 軸方向の力の大きさを表します。
2行目は \(y=0\) の \(zx\) 平面上にある立方体の面の対面に作用している力を表します。
\(S_{yx}\) は \(x\) 軸方向の力の大きさを表します。
\(S_{yy}\) は \(y\) 軸方向の力の大きさを表します。
\(S_{yz}\) は \(z\) 軸方向の力の大きさを表します。
3行目は \(z=0\) の \(xy\) 平面上にある立方体の面の対面に作用している力を表します。
\(S_{zx}\) は \(x\) 軸方向の力の大きさを表します。
\(S_{zy}\) は \(y\) 軸方向の力の大きさを表します。
\(S_{zz}\) は \(z\) 軸方向の力の大きさを表します。
単位法線ベクトルで表される面の方向ベクトルに応力テンソルを作用させると、その面に作用している応力を取り出すことができます。
 圧縮力や引張力によるひずみ ( 垂直ひずみ )
圧縮力や引張力によるひずみ ( 垂直ひずみ )長さ
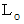 の円柱構造をした軟体の両端に大きさ
の円柱構造をした軟体の両端に大きさ 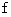 の圧縮力を加えたとき、 長さが
の圧縮力を加えたとき、 長さが 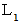 になったとしましょう。 このとき、「 垂直ひずみ 」を次の式で表わすことにします。
になったとしましょう。 このとき、「 垂直ひずみ 」を次の式で表わすことにします。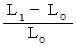
圧縮の場合の「 垂直ひずみ 」は負の数で、 伸展の場合の「 垂直ひずみ 」は正の数になります。
「 垂直ひずみ 」は「 垂直応力 」に比例します。「 垂直応力 」を「 垂直ひずみ 」で割った値を「 ヤング率( 縦弾性係数 )」といいます。(「 圧縮応力 」は負の数で表されます。)「 ヤング率 の高い物質ほど、 圧縮力や引張力による弾性変形を受けにくい。」ということになります。 軸方向の変形には 圧縮変形 と 伸展変形 がありますので、「 ヤング率 」には「 圧縮ヤング率 」と「 伸展ヤング率 」があります。 しかし、 一般的には「 ヤング率 」とは「 伸展ヤング率 」のことを言います。
 ずり力によるひずみ( 剪断ひずみ )
ずり力によるひずみ( 剪断ひずみ )「 剪断ひずみ 」のモデルは、 分厚く重ねたコピー用紙の両横側面を反対方向にこすって、 その直方体の形の高さを変えないで前後側面が平行四辺形になった形に崩すことです。 そのときの底面に対する上面の変位を高さで割った値が「 剪断ひずみ 」になります。「 剪断ひずみ 」は「 剪断応力 」に比例します。「 剪断応力 」を「 剪断ひずみ 」で割った値を「 剪断弾性係数( 横弾性係数 )」といいます。「 剪断弾性係数 の高い物質ほど、 ずり力による弾性変形を受けにくい。」ということになります。
 屈曲力によるたわみ ( ひずみとは言いません )
屈曲力によるたわみ ( ひずみとは言いません )簡易的には、「 円柱の中央部の両端を結ぶ線分からの距離 」を「 円柱の両端を結ぶ線分の長さ 」で割った値で、 たわみの程度を表しませんか?
正確には、 両端の支え方や垂直ひずみを考慮した、 たわみの度合いを表す式があります。
 捻転力によるひずみ
捻転力によるひずみ捻転させると剪断応力が働きますので、「 剪断ひずみ 」を応用させた「 捻転ひずみ 」の式を次のように作りませんか?
円柱の長さを
 、 底面の直径を
、 底面の直径を 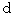 、 両端の相対的捻転角を
、 両端の相対的捻転角を  とすると、
とすると、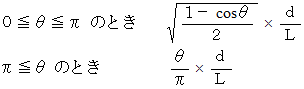
-
いろんな素材でできた円柱物質を永久に変形させようとする力に対する抵抗力は、 実際に力を加えた後に力を抜いて、 元の形に戻らなくなる最小の力を測定して求められます。 その値は「 強度 」と言われます。 いくらひずんでもたわんでも元に戻れば、 その物質の「 強度 」は大きいことになります。
- 圧縮力に対する強度 :
- 圧力で表される。 単位は、
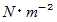 。
。- 引張力に対する強度 :
- 負の圧力の絶対値で表される。 単位は、
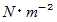 。
。- 屈曲力に対する強度 :
- 力のモーメントで表される。 単位は、
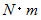 。
。例えば、 長さ
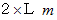 の板の両端を固定し、 ちょうど板の真ん中に
の板の両端を固定し、 ちょうど板の真ん中に 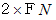 以上の力を加えた後に力を緩めたところ板が変形してしまう場合は、 強度は
以上の力を加えた後に力を緩めたところ板が変形してしまう場合は、 強度は 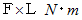 になる。
になる。- 捻転力に対する強度 :
- 力のモーメントで表される。 単位は、
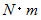 。
。 材料力学 へ戻る
材料力学 へ戻る