（１） 抽出した中にお目当ての物が入っている確率

【 問 題 】
　 整数 ０ 〜 ９ が書かれたカードが １ 枚ずつ全部で10枚あります。
　 無作為に３枚のカード抽出したとき、 その中に０のカードが入っている確率は？

【 解 答 】
　 すべての場合の数 ：　₁₀Ｃ₃ ＝ 10*9*8 / 3*2　とおり
　 ０のカードが入っている場合の数 ：　₉Ｃ₂ ＝→　9*8 / 2　とおり
　　　　　　　　　　　　　　　　　　　　　　　※ ０以外のカードから２組を選ぶ場合の数
　 したがって、 答えは、　9*8*3*2 / 2*10*9*8　＝→　3 / 10　です。

　　 整数 ０ 〜 ９ が書かれたカードが １ 枚ずつ全部で10枚ある中から
　 ｎ 枚のカード抽出するとき、（ 1 ≦ ｎ ≦ 10 ）、
　 その中に０のカードが入っている確率は次のようになります。
　　　



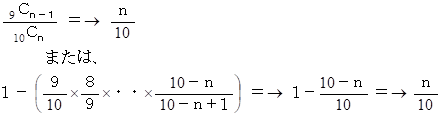
（２） ２段階的抽出

　 赤玉が １ 個 と 白玉が９個あります。
　 無作為に １ 個の玉を抽出したとき、 それが赤玉であれば、 当たりとします。
　 まず、 10個の玉から無作為に ｎ 個 の玉を選びます。
　 １ ＜ ｎ ＜ 10 とします。
　 次に、 選んだ玉の中から無作為に １ 個 の玉を選びます。
　 それが当たりになっている確率は　n / 10　*　1 / n　＝→　1 / 10　です。



（３） 抽出した中にお目当ての物は何個入っている？

【 問 題 】
　 抽出対象数 ｎ 個 のうち、 お目当ての物の数は ｍ 個です。 無作為に ｋ 個抽出したとき、 平均してお目当ての物は何個入っているでしょうか？

【 解 答 】
　 求める答えは、 1 個を選んだときにお目当ての物である確率の ｋ 倍です。
　 その確率は　ｍ / ｎ　ですから、 答えは　ｋｍ / ｎ　です。
その理由：
　 お目当ての物　その１、その２、その３、・・・ そのｍ までのｍ個。
　 ｋ 個抽出したとき、 お目当ての物 その１ のみをgetする確率は ｋ / ｎ
　 この場合、お目当ての物が１個のみ入っているので、
　 お目当ての物をgetする数の期待値は 1 × ｋ / ｎ
　 ｋ 個抽出したとき、 お目当ての物 その２ のみをgetする確率は ｋ / ｎ
　 この場合、お目当ての物が１個のみ入っているので、
　 お目当ての物をgetする数の期待値は 1 × ｋ / ｎ
　 同様のことがｍ個のすべてのお目当ての物について言えるので、
　 全体としてお目当ての物をgetする数の期待値は ｋｍ / ｎ になります。

＜ シミュレーション ＞

　 全部のくじの数（ｎ）：　
　 当たりくじの数（ｍ）：　
　 引くくじの数（ｋ）　：　

　　　　　　

　 当たりくじの入っていた確率 ：　
　　　　　理論値 ＝ １−（ _ｎ−ｍＣ_ｋ ÷ _ｎＣ_ｋ ）＝
　 平均して何個の当たりくじが入っていたか ：　 個

　

プログラムの内容 ：

（４）　抽出した中にお目当ての物が入っていない確率

【 問 題 】
　 くじＡは10個 のうち当たりが １ 個です。 くじＢは２０個のうち当たりが２個です。 ４回続けてくじを引いたとき（ 一度引いたくじは元に戻しません ）、 外ればっかりの確率はどちらが大きいですか？
　　　ａ． 同じ
　　　ｂ． くじＡ
　　　ｃ． くじＢ

【 解 答 】
　　 答えは ｃ です。

　　
　　

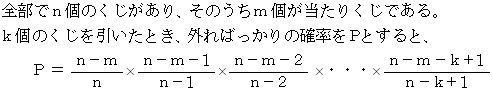
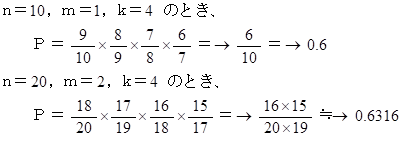
　　さきほどのシミュレーションで確かめてみてください。
　「 当たりくじの入っている確率 」が異なることが分かると思います。