基礎物理学 へ戻る（１） 音の高さ（ ピッチ ） 決めているのは、 波長でなくて周波数だ
-
空気中を伝わる音の速さは
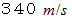です。音源から観察者に向かう方向をプラス方向とし、 空気に対する音源の移動の速さを
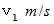とし、 空気に対する観察者の移動の速さを 
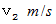とすると、 音源が発する 
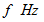の音は、 観察者には次のような周波数として聞こえます。 これはドップラー効果と言われます。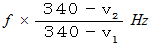
地面に対して無風の状況であるとします。（ 空気に対する音源や観察者の移動の速さを用いると宣言している。）
地面に対して静止している音叉が
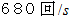振動しているために、 音が発生しています。 観察者Ａ は、 地面に対して静止しています。 このとき、 観察者Ａ が聞く音の周波数と波長は次のようになります。
観察者Ｂ は、 音叉に対して速さ
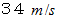で近づいています。 このとき、 観察者Ｂ が聞く音の周波数は次のようになります。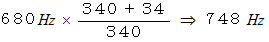
このとき、 観察者Ｂ の立場で考えると、 観察者Ｂ に対して、 速さ
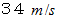の風が吹いていることになります。 したがって、 風上から聞こえてくる音の速さは 
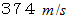です。 したがって、 観察者Ｂ が聞く音の波長は次のようになります。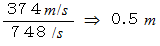
観察者Ａ にとっても観察者Ｂ にとっても波長は同じです。 この考察より、 音の高さを決めているのは、 波長でなくて周波数であることがわかります。
-
今度は、 音叉が観察者Ａ に対して速さ
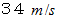で近づいています。 このとき、 観察者Ａ が聞く音の周波数は次のようになります。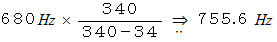
このとき、 観察者Ａ に対して風は吹いていません。 したがって、 音の速さは
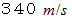です。 したがって、 観察者Ａ が聞く音の波長は次のようになります。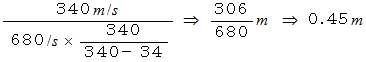
以上のように、 観察者Ａ にとって、 音叉が静止しているときと移動しているときとでは、 波長は異なります。 しかし、 このとき周波数も異なっていますから、 音の高さを決めているのは、 周波数でなくて波長であるとは言えません。
（１）では、 音速が変化することによって周波数のみが変化しましたが、（２）では、 音速が変化しないで、 波長と周波数が同時に変化しています。 これは、 空気に対して音叉も観察者も静止しているときに、 音叉の振動数を変化させることによって、 音速を変化させないで波長と周波数を同時に変化させるのに似ています。
（１）のドップラー効果を、 私は 音速変化性ドップラー効果 」 言い、（２）のドップラー効果を「 音速非変化性ドップラー効果 」と言い、 ２つがミックスしたものを「 混合性ドップラー効果 」と言っています。
-
（１）の考察では、 観察者Ｂ は観察者Ａ に対して、 音速が大きく、 かつ、 音の振動数が大きくなっていました。 そこで、 音の伝わる速さが空気の約３倍であるヘリウムガスで置換された部屋の中で、 レコードを聴いてみましょう。 もしかしたら全体のピッチが１オクターブ半ほど上がっているかもしれません。 しかし、 これは大がかりな実験なので専門家にお任せすることとして、かわりに次のような思考実験をしてみましょう。 680回/s の速さで振動している音叉は、 音叉に接している空気の微小空間Ｐの音圧を
秒 から 
秒 までの１秒間に680回周期的に変動させます。 その 秒における微小空間Ｐの音圧の微小変化が観察者に伝わってくる時刻が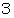 
秒 であった場合には、 秒における微小空間Ｐの音圧の微小変化が観察者に伝わってくる時刻は （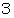 
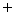
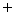
）秒となります。 空気をヘリウムガスに置換して行うと、 秒における微小空間Ｐの音圧の微小変化が観察者に伝わってくる時刻は 秒であり、 秒における微小空間Ｐの音圧の微小変化が観察者に伝わってくる時刻は （ ）秒となります。 したがって、 空気であってもヘリウムであっても、 観察者が聞く音の周波数は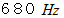 
となります。 したがって、 媒体によって音の伝わる速さが違うからといって、 媒体によって音源が発する音の音高が変化するということはないのです。光が空中から水中に入ってもその色は変わりません。音が空中から水中に入ってもその高さは変わりません。それは、人間が光や音を波長で感じているのではなく、振動数で感じているからです。
-
観察者を「 主観的非移動者 」として捉えると、 次の波の塊が単位時間当たりに観察者に飛び込んでくることになります。
標準 ：
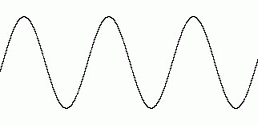
音速変化性ドップラー効果（ 音の速さで観察者が音源に近づく場合 ） ：
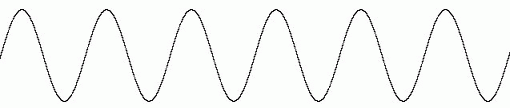
音速非変化性ドップラー効果（ 音の速さの半分で音源が観察者に近づく場合 ） ：
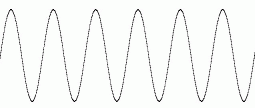
「 媒体の置換による音速の変化 」（ 音の速さが標準の２倍の媒体になった場合 ） ：
-
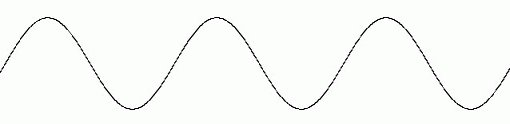
ヘリウムガスで置換されたドーム球場の中では、 空気中でのドップラー効果と同じ効率で周波数を増やすためには、 約３倍の速さで観察者は移動しなければなりません。
