問題 :
-
( SI単位系であるが、 単位を省略している。)
内腔の半径の長さ R の球を半分に切ったお椀がある。 その中で、 質量 m の球が、同じ高さをずっと保ったまま、 角速度 ω で等速円運動をして転がっている。 球はお椀に比べて著明に小さいものである。
このとき、 球の軌道の高さ( お椀の底を基準とする )と お椀から受ける抗力の大きさ を求めよ。
-
下図のように角度 θ をとる。 また、 球の軌道の高さを h とし、 抗力の大きさを N とする。 球に対して静止している観察者の視点で考えると、 球に働いている力には、 お椀の抗力以外に、 鉛直方向の重力 と 水平方向の遠心力 がある。 重力 と 遠心力 を合成した力がお椀に作用しているのであるが、 その反作用としてお椀が球に及ぼす力が抗力である。
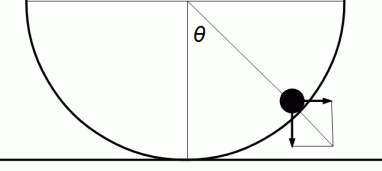
球に作用している重力の大きさ : mG ( G は重力加速度 )
球に作用している遠心力の大きさ : m ×( R sinθ )× ω2
重力のお椀の接線方向成分 と 遠心力のお椀の接線方向成分 の合力は 0 であるから、
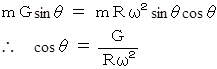
一方、
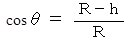
したがって、
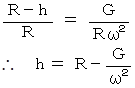
以上で球の軌道の高さが求まった。 次は抗力であるが、 次の式が成り立っている。
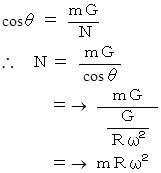
 力学 へ戻る
力学 へ戻る