今から4000年前の人は、 満月を見ながら考えた。「 円周の長さは直径に比例しているんじゃないか？」と考えた。 そして、 いろんな長さの紐と２本の小枝を用いて、 土にいろんな大きさの円を描き、 比例定数を求めようとした。 その比例定数が円周率である。

　 日本が江戸時代のころ、 西洋人は考えた。「 円は中心角が360度の扇形なのだ。」と。それからこうも考えた。「 扇形の弧の長さは、 半径にも中心角にも比例している。 扇形の半径と中心角は互いに独立なので、 扇形の弧の長さは、半径と中心角とを掛け合わせたものに比例している。」と。 そして、 彼らはその比例定数を求めたはずだ。 さらに彼らは考えた。「 いっそのこと比例定数が １ になるように、 新たな角度の単位を作ろう。」と。 それが弧度法である。

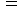
　 したがって、 半径と弧の長さが等しい扇形の中心角が「 １ ラジアン 」になった。 １ ラジアンは およそ57度 である。 中心角が180度の扇形（ それは半円であるが ）の中心角（ それは180度であるが ）を「 ラジアン 」とすれば、 その扇形の弧の長さは 「 × 半径 」 となる。 ということは、 円の円周の長さは「 ２ × × 半径 」になる。 この式 と 4000年前の人が考えた「 円周の長さ ＝ × 直径 」とを比べてみると、「 」になる。 したがって、「 ラジアン ＝ 180度 」である。「 ＝ 180度 」ではない。「 ＝ 3.141592・・・・ 」である。