レーザー光は、 屈折や反射を含めて、 最短時間で、 ある場所から他の場所へ伝わっていきます。 この原理を用いて、 パラボラアンテナの軸に水平に入ってきた光はすべて反射されて焦点を通過することを証明してみます。
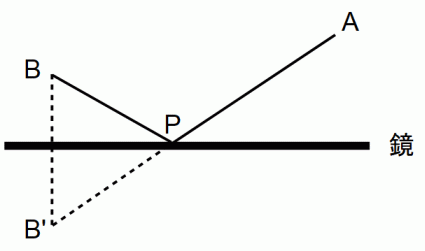
上図のように、 点Aから鏡に向けてレーザー光を発射させ、 反射した光が点Bを通過するようにします。 そのとき、 鏡上の光が反射した点をPとします。 点Pが鏡上を自由に移動できると仮定したとき、 図の点Pは、 光の最短経路となっています。 そしてこのとき、 光の入射角と反射角は等しくなっています。
パラボラアンテナの原理 :
y 軸に平行に入ってきた光は、 放物面で反射されて焦点に向かう。
-
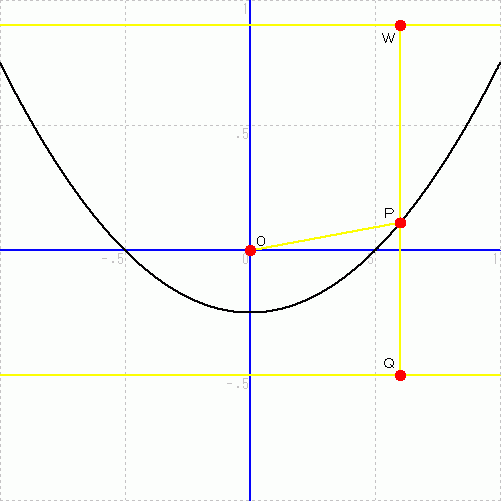
放物線 y = x2− 1/4 の焦点は原点にあります。
ОP = QP ( 放物線の定義より )
WQ = WP + ОP
WQ がどんなに真横にスライドしても上記の関係は維持されます。
したがって、 y 軸に平行に入ってきた光が放物線に当たる点における放物線の接線に対して、 光の入射角と反射角は等しくなっています。 したがって、 y 軸に平行に入ってきた光はすべて、 放物面で反射されて焦点に向かいます。
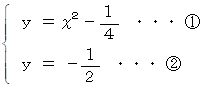
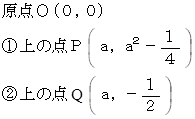
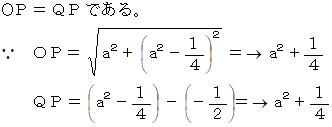
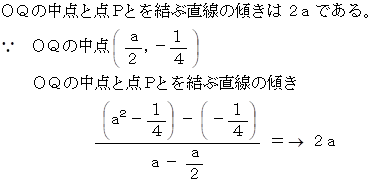
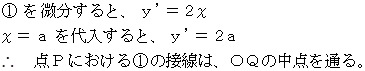
 図形の方程式 へ戻る
図形の方程式 へ戻る