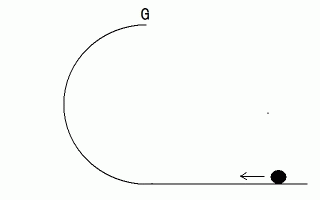
上の図のようなレールがあります。 左側の半円の直径は
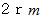 です。 質量
です。 質量 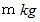 の玉を初速
の玉を初速 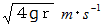 で左方向に打ち出します。 その後、 この玉はどんな移動をするでしょうか。 摩擦はないものとします。
で左方向に打ち出します。 その後、 この玉はどんな移動をするでしょうか。 摩擦はないものとします。平地を移動している間は、 玉の運動エネルギーは
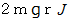 です。 エネルギー保存の法則より、 運動エネルギーをすべて位置エネルギーに変換させれば、 玉は
です。 エネルギー保存の法則より、 運動エネルギーをすべて位置エネルギーに変換させれば、 玉は 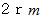 の高さまで上昇できます。 したがって、 答えは、 「 レールの頂点
の高さまで上昇できます。 したがって、 答えは、 「 レールの頂点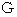 に近づくにつれて減速し、 頂点
に近づくにつれて減速し、 頂点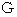 に到着した瞬間は速さ
に到着した瞬間は速さ 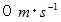 で、 それから真下に落下する。」 となります。
で、 それから真下に落下する。」 となります。残念、 それは正解ではありません。 玉は頂点まで達せず、 途中でレールを離れて右向きに放物線を描いて落下します。「 えっ、 エネルギー保存の法則が成り立ってないじゃない。」と言われる方へ、 玉がレールを離れる瞬間、 玉は右向きに移動しており、 運動エネルギーは
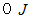 ではありません。
ではありません。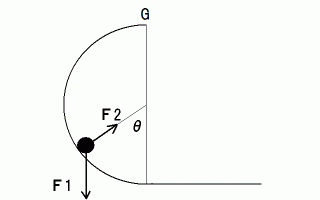
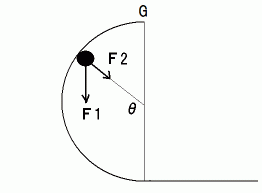
上の図たちは、 玉が
 の角度まで上昇した瞬間に、 玉に作用している力を描いたものです。
の角度まで上昇した瞬間に、 玉に作用している力を描いたものです。 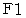 は重力で、
は重力で、 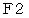 はレールからの抗力です。 向心力は次のようになります。
はレールからの抗力です。 向心力は次のようになります。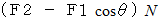
このときの玉の速さを
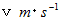 としますと、 非等速円運動( 軌道拘束あり )の速さと向心力の関係から、 向心力は次のようになります。
としますと、 非等速円運動( 軌道拘束あり )の速さと向心力の関係から、 向心力は次のようになります。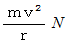
したがって、次の式が成り立ちます。
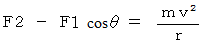
玉が頂点
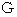 に到達するためには、
に到達するためには、 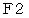 が頂点
が頂点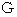 に達した時に
に達した時に  以上になっていなければなりません。
以上になっていなければなりません。  のとき、 上式は次のようになります。
のとき、 上式は次のようになります。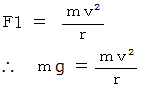
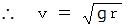
したがって、 かろうじて頂点
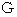 に到達した玉の速さは
に到達した玉の速さは 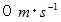 ではなく、
ではなく、 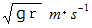 です。 このとき、 玉のエネルギーは次のようになります。
です。 このとき、 玉のエネルギーは次のようになります。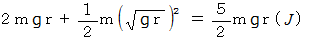
したがって、 玉を頂点
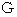 に到達させるには、 最初に少なくとも
に到達させるには、 最初に少なくとも 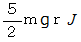 の運動エネルギーを与えなければならず、 そのためには初速は
の運動エネルギーを与えなければならず、 そのためには初速は 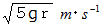 以上必要です。
以上必要です。< 他の考え方その1 >
玉の速さを
 とすると、 遠心力は次のようになる。
とすると、 遠心力は次のようになる。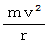
したがって、 抗力は次のように表される。
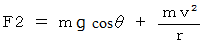
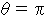 のときに、
のときに、 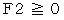 でなければならないので、
でなければならないので、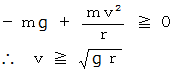
< 他の考え方その2 >
頂点Gに達した瞬間の玉の速さを
 とする。 このとき、 遠心力の大きさが
とする。 このとき、 遠心力の大きさが重力の大きさ以上であればよいのだから、次の式が成り立てばいいことになる。
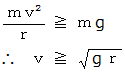
 力学 へ戻る
力学 へ戻る