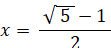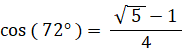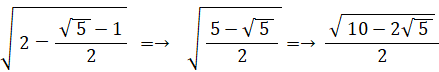cos 72°
 三角関数 指数・対数関数 へ戻る
三角関数 指数・対数関数 へ戻る
 大学生のための数学 へ戻る
大学生のための数学 へ戻る
2023.05.04____
円に内接する正5角形
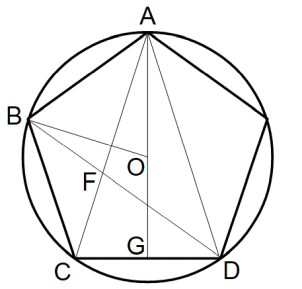
∠CAD = 36°
∠FDC = 36°
∠CBD = 36°
∠ACB = 36°
∠AOB = 72°
∠ACD = 72°
∠ADC = 72°
∠DFC = 72°
∠DCF = 72°
よって、△ACD と △ DFC は相似である。
また、FA = FD = CD
AC = 1 , CD = x と置く。
AC:CD = DF:FC より、 1 : x = x : 1 −x
よって、 x2 + x − 1 = 0 したがって、
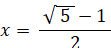
cos (72°) = CG / AC =→ CG かつ CG = CD / 2 だから、
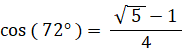
ちなみに、正五角形の重心から頂点までの距離を 1 とすると、一辺の長さは、余弦定理より、次の式の正の平方根になることが分かります。
12 + 12 − 2×1×1×cos (72°)
つまり、
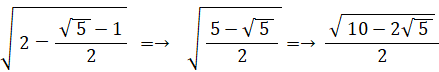

 三角関数 指数・対数関数 へ戻る
三角関数 指数・対数関数 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る