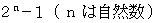 は メルセンヌ数 と言われます。 メルセンヌ数は次のように展開することができます。
は メルセンヌ数 と言われます。 メルセンヌ数は次のように展開することができます。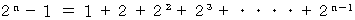
これは、 初項 1 、公比 2 の等比数列の総和の公式から導かれます。
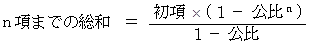
また、 メルセンヌ数を2進数にしますと、 すべての桁が1になります。
メルセンヌ数のうち素数であるものは、 メルセンヌ素数 と言われます。 オイラーは、 メルセンヌ素数を
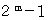 とすると
とすると 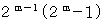 が 完全数 になることを発見しました。 完全数とは、 自分以外の約数の総和が自分に等しい自然数のことです。 彼がどのようにしてこの定理を発見したのか、 考えてみましょう。
が 完全数 になることを発見しました。 完全数とは、 自分以外の約数の総和が自分に等しい自然数のことです。 彼がどのようにしてこの定理を発見したのか、 考えてみましょう。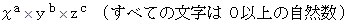 で表される自然数の約数の総和は、 次の公式を用いて求めることができます。
で表される自然数の約数の総和は、 次の公式を用いて求めることができます。
この公式より、
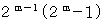 の約数の総和は次のようになります。
の約数の総和は次のようになります。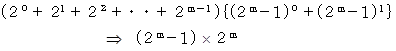
約数の総和から自分自身を引くと、 次のようになります。
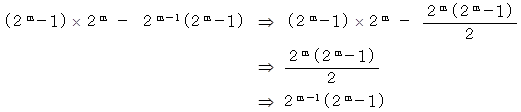
以上より、
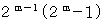 が完全数になっていることが解りました。
が完全数になっていることが解りました。以下に メルセンヌ素数を求める十進BASIC のプログラム と 完全数を求める十進BASIC のプログラム を紹介します。
完全数を求める十進BASIC のプログラムソースは、 としさんのブログよりいただきました。
http://okadatoshi.exblog.jp/
このプログラムのアルゴリズムは次のようになっています。
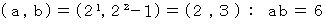 は完全数である。
は完全数である。
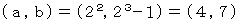

 は 素数か? ( 3の倍数か? )
は 素数か? ( 3の倍数か? )  素数である。
素数である。
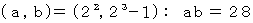 は完全数である。
は完全数である。
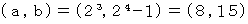

 は 素数か? ( 3の倍数か? )
は 素数か? ( 3の倍数か? )  素数ではない。
素数ではない。
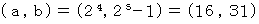

 は 素数か? ( 3の倍数か? でなければ5の倍数か? ・ ・ ・ )
は 素数か? ( 3の倍数か? でなければ5の倍数か? ・ ・ ・ )  素数である。
素数である。
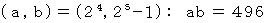 は完全数である。
は完全数である。
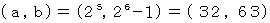
 十進
十進