と と は１００以下の自然数とします。　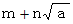 の逆数が 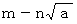となる と と の組み合わせをすべて書き出してみましょう。 次のような十進BASIC のプログラムを作って実行します。 四捨五入関数を使用している理由は、 微妙に １ と異なる数が出力されてしまうからです。

ペル方程式は、次のようなものです。
　　　　　　

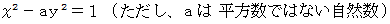
ペル方程式は次のようにも書くことができます。
　　　　　

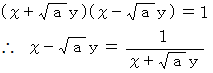
　 ペルの方程式の解の１つに 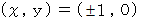が存在することはすぐにわかると思います。 それでこの解は 「 自明の解 」 と言われます。 しかし、 自明でない解はなかなか見つけにくいものです。

　 たとえば　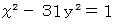　の解を求めてみましょう。
それには、 次のようなプログラムを組んで実行します。

　 自明でない解は 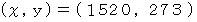であることが解りました。 しかし、 それにしても、 この計算時間の長さはなんとかならないものでしょうか。

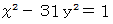　 　は次のように変形されます。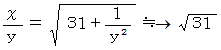
　　　　　
　 この式の意味は、 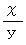が に近い値をとるということです。 ということは、 に近い分数を探して、 その分子と分母が解の組になっているかどうかを確かめればいいということです。 そのためには、 の連分数をとってから近似分数を求める方法があります。