囲碁の領地の広さは囲んでいる格子の交点の数で表されます。 これと同様に、 図形の面積も単位幅の格子の交点の数で表すことが出来ないものでしょうか？　約100年前のことです、 ピックは次のような提案をしました。

　「 図形の中に存在する単位格子の交点の合計 」と「 頂点または辺の上に存在する単位格子の交点の合計を２で割ったもの 」を加えて、それから １ を引いたもの　がほぼ図形の面積に等しくなっている。


　　　　　　


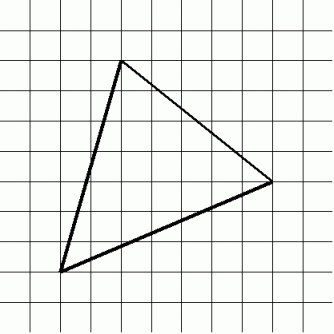
上の三角形を彼の提案に当てはめると、
　　　　　
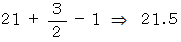
実際に面積を求めて見ると、
　　　　　

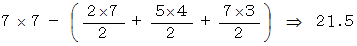
　 このケースではぴったりと一致しましたね。 では、 一辺の長さが ７ の正方形の場合はどうでしょうか。
　　　　　
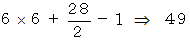
　 この場合もぴったりと一致しましたね。 というわけで、 彼の提案は「 ピックの定理 」と言われています。