比較的大きな約数を求めるためのプログラムです。

全体集合を自然数とする。　Ｋ， Ｑ， Ｗ　の３つの数がある。

（ Ｑ と Ｗ の差 ） と Ｋ とに 最大公約数 Ｐ が存在するとき、
　　　Ｋ　＝　ａ × Ｐ
　　　Ｑ　＝　ｂ × Ｐ ＋ d
　　　Ｗ　＝　ｃ × Ｐ ＋ d



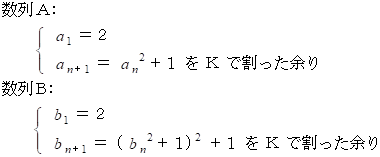
　 ｎ ＝ １ から １ つずつ ｎ を大きくしていきながら、 ペア 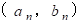の差 と Ｋ とが互いに素でないものを １ つ発見するまで続け、 そのときの 最大公約数 を Ｋ の約数とする。

　 以上が、 上記のプログラムのアルゴリズムになっています。


＜ ポラード・ロー素因数分解法 の デモンストレーション（ JavaScript ＋ html のプログラム ）＞

　




プログラムの内容 ：