（１） ポアソン分布の導入のために必要な式

　　　



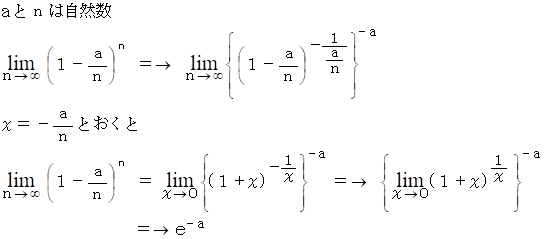
（２） ポアソン分布の理解のために大切な誤解答

【 問題 】

　 ある患者に起こる心室性期外収縮 （ ＶＰＣ ） について ：　起こるのは一瞬で、 起こる間隔は 10 分以上。 １ 日のうちランダムな時刻に起きる。 １ 日必ず３回だけ起きる。
　 このＶＰＣを心電図で捉えたい。 しかし、 心電図で監視できる時間が次のように決められている。
　 時刻を分で表したとき （ 例えば 2:30 は 150 分 になる ） 10ｔ 〜 10（ ｔ＋１ ） 分　（ ｔは０から 143 までの整数 ） の 10 分間 を １ 枠とし、 それを １ 日６枠の 計 60 分間。

　ア． 何回ＶＰＣを心電図で捉えることが望めるか、 その期待値は ？
　イ． １回だけＶＰＣを心電図で捉えることのできる確率は ？
　ウ． ２回だけＶＰＣを心電図で捉えることのできる確率は ？
　エ． ３回すべてのＶＰＣを心電図で捉えることのできる確率は ？
　オ． １回もＶＰＣを心電図で捉えることのできない確率は ？

【 誤解答 】

心電図で監視できる時間帯は、１日のうちに 144 枠 のうちの６枠である。
１枠においてＶＰＣを心電図で捉えることのできる確率（ Ｐ ）は 3 / 144

　ア． 期待値 ：　６×Ｐ　＝→　0.125 回
　イ． １ 回だけの確率　_６C₁ × Ｐ ×（１−Ｐ) ⁵　≒→　11.2511 %
　ウ． ２回だけの確率　_６C₂ × Ｐ ² ×（１−Ｐ) ⁴　≒→　0.5985 %
　エ． ３回ともの確率　_６C₃ × Ｐ ³ ×（１−Ｐ) ³　≒→　0.0170 %
　オ． １ 回もＶＰＣを心電図で捉えることのできない確率の答えは２つある！？
　　　　　100　−（ 11.2511 + 0.5985 + 0.0170 ） ≒→ 　88.1334 %
　　　　　(１−Ｐ) ⁵　≒→　88.1332
　　 の方が正解だと思いますが ・ ・ ・ ・ 。

【 解 説 】

　 以上の解答はすべて間違いです。 なぜなら、１回目の心電図での監視終了時点でＶＰＣを心電図で捉えることのできる確率Ｐが変化するからです。 つまり、 この場合は、 サイコロを何回も振る場合とは違います。 独立事象の反復確率ではないのです。
ただし、 答えが間違いであるといっても、 正解の近似値にはなっています。
１ 回もＶＰＣを心電図で捉えることのできない確率の正解はというと、
　　　（ １− 3 / 144 ） × （ １− 3 / 143 ） × （ １− 3 / 142 ） × （ １− 3 / 141 ） × （ １− 3 / 140 ） ×（ １− 3 / 139 ）
　　　　≒→　87.9330 %

（３） ポアソン分布

【 問 題 】

ある患者に起こる心室性期外収縮（ＶＰＣ）について：　起こるのは一瞬。 平均１日３回起きる。
１年間（ 365日間 ）ずっと心電図で監視する。
ＶＰＣが１回も起こらない日、ＶＰＣが３回だけ起こる日、ＶＰＣが６回だけ起こる日、
それぞれ１年間に何日あるか、その期待値を求めよ。

【 解 答 】

　 ＶＰＣが１日３回だけしか起こらないのとは違います。 また、観察時間も継続的です。 ＶＰＣが起こった直後に今後のある時間幅にＶＰＣを心電図で捉えることのできる確率が変化するわけでもありません。 このような場合には、 心電図で監視する時間枠の幅を極限まで短くして枠数を無限に増やした上で、 二項分布を使って確率を求めるというのがポアソン分布の考え方です。 １枠で目的物を発見する確率は限りなく０に近くなっていますが、 目的物を発見する枠の組み合わせが無数にありますので、 全体としての確率は０に近くはならないのです。

ポアソン分布とは、 確率分布としての二項分布のｎを無限大にしたものです。

　

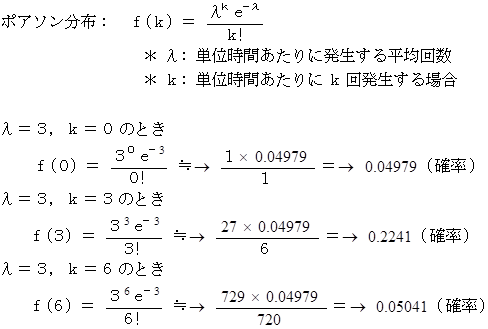
　したがって、 答えは、
　　　　

（４） ポアソン分布を導く

　　　



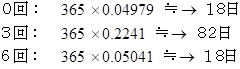
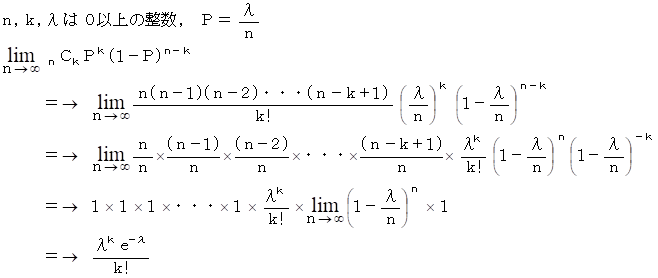
（５） ポアソン分布のシミュレーション

精度 :　 １倍　　 ５倍
ＶＰＣ が 平均して１分間に （ ３〜９ ）回 出現する患者モデル
10 万回の試行

　　　　

　


プログラムの内容 ：