（１） 無限等比数列の和

　　
これは、 初項が 、 公比が の等比数列です。

を求めてみましょう。
　　　　
　　　　

を求めてみましょう。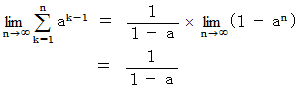
　　　　

この式は次のようにも書くことができます。
　　　　
のときは、 上の式は次のようになります。
　　　　

　 を展開してみましょう。
　　　　

（２） 黒体放射の電磁波のスペクトル

　 すべての波長の電磁波を吸収する物質（ 黒色をしています ）に熱を加えると、 スペクトルをもつ電磁波を放射します。 そのうち一番振動数の大きい電磁波に注目しますと、 黒体から輻射される電磁波のエネルギーは、 次の式で表されます。 これを 「 プランクの法則 」 といいます。
　　　　
　　　　　　　　　　　　　　　　　　　　　　　　

　 この式を発見したのがプランクであり、 この式に現れる定数 は、 実験結果から であり、 後に 「 プランク定数 」 と呼ばれるようになりました。

　は、　　ですから、 次のように展開できます。

　　
　 これは、 量子力学的に大変興味深いことです。 は電磁波の粒子が１個存在する場合のエネルギーに関する基本的数値であり、 は電磁波の粒子が２個存在する場合のエネルギーに関する数値であり、 は電磁波の粒子が３個存在する場合のエネルギーに関する数値であり、 そしてそれらを無限に加えたものが全体としてのエネルギーに関する数値になっているということです。 これは、 電磁波が波であるにもかかわらず、 粒子としての性質も持っているということです。 プランクはこのように考え、 アインシュタインよりも先に「 光粒子説 」を発表したのです。 それは1900年のことでした。