まずは、 空気がないと仮定した時の自由落下運動から考えてみましょう。
初速を
 とし、 スタート地点からの距離を
とし、 スタート地点からの距離を  、時間を
、時間を  として、 運動方程式を立てます。
として、 運動方程式を立てます。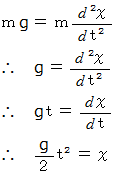
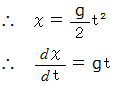
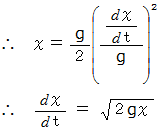
( 横軸 :
 , 縦軸 :
, 縦軸 :  )
)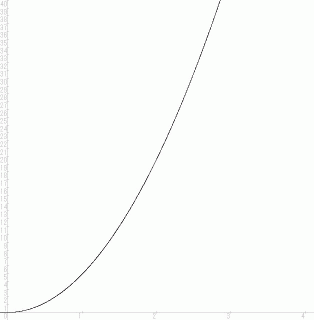
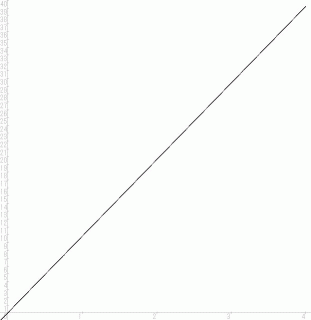
( 横軸 :
 , 縦軸:
, 縦軸:  )
)
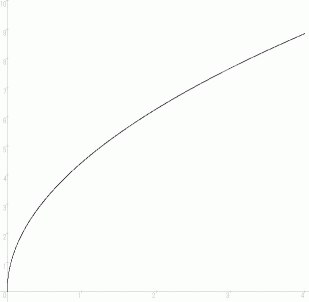
( 横軸 :
 , 縦軸 :
, 縦軸 :  )
)
今まで考えたのは真空状態の場合ですが、 現実的な落下には空気抗力が作用しますのでこれとは異なります。
次の式で与えられる空気抗力があるとき、 ( 空気抵抗は移動している物質の速さの2乗に比例します。 質量とは無関係です。)
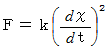
質量

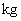 の物質を初速
の物質を初速  で落下させたときの、 スタート地点からの距離を
で落下させたときの、 スタート地点からの距離を  、 時間を
、 時間を  として、 運動方程式を立てます。
として、 運動方程式を立てます。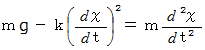
この一次常微分方程式を解くのは困難です。 そこで、 この式の両辺が
 になるのはどんな場合か考えてみましょう。
になるのはどんな場合か考えてみましょう。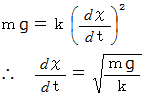
つまり、 速さが上のようになった時に、 落下速度の大きさは一定になるということです。 そして、 質量の大きな物質のほうが、 一定になったときの速さが大きいということです。 というわけで、 現実では、 質量の大きな物質のほうが速いスピードで短時間に落下します。
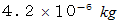 の質量の雨粒は
の質量の雨粒は 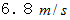 の速さで地上に衝突するというデーターがあります ( 本当かどうかは確認していません ) ので、 これより湿度の高い空気の
の速さで地上に衝突するというデーターがあります ( 本当かどうかは確認していません ) ので、 これより湿度の高い空気の 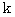 の値を推測しますと、 次のようになります。
の値を推測しますと、 次のようになります。
 力学 へ戻る
力学 へ戻る