(1) 媒介変数で表される曲面の面積
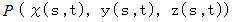 で表される曲面があります。
で表される曲面があります。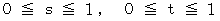 の範囲における曲面の表面積は、 次の式で与えられます。
の範囲における曲面の表面積は、 次の式で与えられます。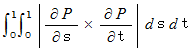
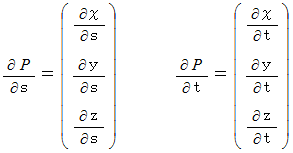

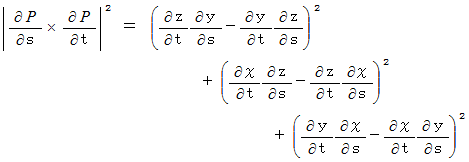
-
ドーナッツを真半分に切ると、 その片方の切断面は2つの半径
 の円になるとします。 すると、 この断面の円の円周の長さは
の円になるとします。 すると、 この断面の円の円周の長さは 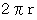 になります。 また、 この切断面の中心からドーナッツの重心までの距離を
になります。 また、 この切断面の中心からドーナッツの重心までの距離を 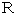 とします。 すると、 その距離を半径とする円の円周の長さは
とします。 すると、 その距離を半径とする円の円周の長さは 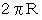 になります。 するとドーナッツの表面積は次の式で表されます。
になります。 するとドーナッツの表面積は次の式で表されます。ドーナッツの表面積 :
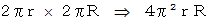
これは道の面積の応用です。 この式を導いてみましょう。
このドーナッツを水に浮かべると、 ちょうど半分が水に浸かった状態で水面に浮きました。 水面を

 平面とし、 ドーナッツの重心を通る鉛直方向の直線が
平面とし、 ドーナッツの重心を通る鉛直方向の直線が 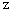 軸を作るものとします。
軸を作るものとします。水面に
 軸と
軸と  軸をとり、
軸をとり、  軸 から
軸 から  軸 に向かって
軸 に向かって  ラジアンの角度で
ラジアンの角度で 
 平面と交わる
平面と交わる 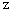 軸を含む平面でドーナッツを切断した時、その切断面 (
軸を含む平面でドーナッツを切断した時、その切断面 ( 
 平面の第1限象にあるところを思い浮かべてください。) の中心から水面に対して
平面の第1限象にあるところを思い浮かべてください。) の中心から水面に対して 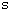 ラジアンの角度だけ
ラジアンの角度だけ 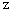 軸の正の方向に回転した絶断面の円周上の点の位置ベクトル
軸の正の方向に回転した絶断面の円周上の点の位置ベクトル 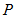 は、 次のように表されます。
は、 次のように表されます。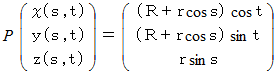
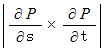 を求めていきます。
を求めていきます。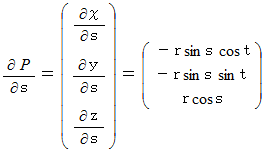
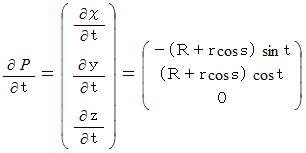
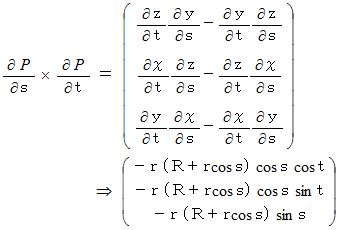
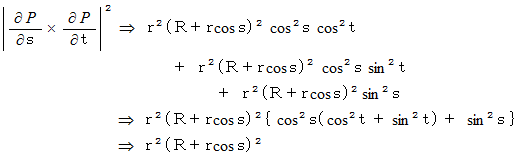
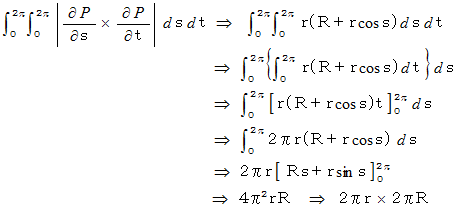
 ベクトル解析 へ戻る
ベクトル解析 へ戻る