分数を連分数に変換する 十進BASIC のプログラムを下枠に紹介します。

少数を連分数に変換する 十進BASIC のプログラムを下枠に紹介します。

>

　 例えば、 6.2413413413413・・・ などの循環小数を入力してみてください。
　 また、 ２の平方根の近似値 1.41421356237309504880 を入力してみてください。 連分数にある規則性があることに気づかれると思います。
　 また、 ネイピア数の近似値 2.71828182845904523536 を入力してみてください。 連分数にある規則性があることに気づかれると思います。
　 また、 円周率の近似値 3.14159265358979323846 を入力してみてください。 次のように出力されます。
　　　　[ 3　7　15　1　292　1　1　1　2　1　3　1　14　2　1　1　2　2　2　3 ]
このプログラムは２０行から先の連分数は出力しませんが、 本当はまだまだ続いています。 292 という比較的大きな数を見ると、 と考えて、 円周率は次の連分数で近似することができることが解ります。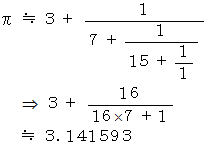
　　　　　

　 しかし、 もっと下の行の分数を０として近似した数に比べると誤差が大きくなっています。

連分数を分数に変換する 十進BASIC のプログラムを下枠に紹介します。

>