maxima では、 次のように入力してリターンキーを押すと、
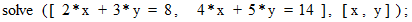
すぐに、 次のような答えが出力されます。
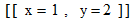
代りに次のような文字式を入力すると、
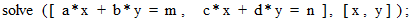
次のような答えを得ることができます。
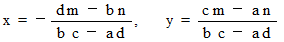
続いて、 次のように順番に1つずつ具体的な値を代入して入力していき、
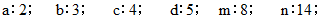
最後に、 次のように入力すると、
 という答えが出力されます。
という答えが出力されます。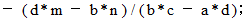
 のとる値がいろいろ変化するときには、 そのたびにいちいち数値を入力していたのでは時間がかかります。 そこで、 十進BASIC を使って次のようなプログラムを作ると作業時間が短縮されます。
のとる値がいろいろ変化するときには、 そのたびにいちいち数値を入力していたのでは時間がかかります。 そこで、 十進BASIC を使って次のようなプログラムを作ると作業時間が短縮されます。DIM M(1,6)
PRINT " a x + b y = c "
PRINT " d x + e y = f "
PRINT " の連立方程式を解きます。"
PRINT " 6つの文字 a, b, c, d, e, f に相当する、具体的な "
PRINT " 数値をコンマで区切って入力してください。"
INPUT PROMPT " a, b, c, d, e, f " : a, b, c, d, e, f
LET x = ( c*e − b*f ) / ( a*e − b*d )
LET y = ( a*f − c*d ) / ( a*e − b*d )
PRINT " x = " ; x
PRINT " y = " ; y
END
十進BASIC には、 逆行列を得る関数や行列に行列をかける演算が標準装備されていますので、 次のようなプログラムでも連立一次方程式を解くことができます。
DIM M(2,3), P(2,2), Q(2,2) ! M は2行3列の行列であることを宣言
DIM X(2,1), R(2,1)
PRINT " a x + b y = c "
PRINT " d x + e y = f "
PRINT " の連立方程式を解きます。"
PRINT " 6つの文字 a, b, c, d, e, f に相当する、 具体的な "
PRINT " 数値をコンマで区切って入力してください。"
MAT INPUT PROMPT "a, b, c, d, e, f " : M
LET P(1,1) = M(1,1)
LET P(1,2) = M(1,2)
LET P(2,1) = M(2,1)
LET P(2,2) = M(2,2)
LET R(1,1) = M(1,3)
LET R(2,1) = M(2,3)
MAT Q = INV ( P ) ! P の逆行列を Q に代入
MAT X = Q * R ! 逆行列を掛ける
PRINT " x = " ; X(1,1)
PRINT " y = " ; X(2,1)
END
< コピぺ用の小窓 >
( 追 伸 )
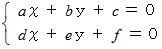
2元連立一次方程式の解の公式の導き方(その1)のガイドラインを示します。
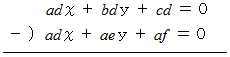
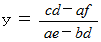
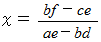
2元連立一次方程式の解の公式の導き方(その2)のガイドラインを示します。
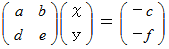
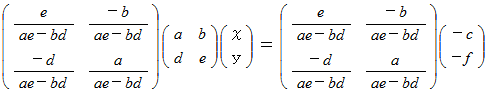
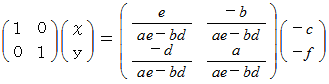
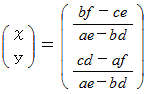
 十進
十進