(1) 条件付き確率
-
条件付き確率とは、「 A → B の2つの時系的事象について、 2つの事象が共に発生する確率 を Bの事象が発生する確率 で割れば、 Bの事象が発生したことが公表された時点でのAの事象が発生していた確率が解る。」という定理です。
-
問題 :
-
上下2つの引き出しの付いた箱が3つあり、 外見は同じです。 箱A には2つの引き出しに黒石が1個ずつ入っています。 箱B には2つの引き出しに白石が1個ずつ入っています。 箱C にはどちらか一方の引き出しに黒石が1個、 他方に白石が1個入っています。 この3つの箱から1つを選んで上の引き出しを開けたところ黒石が入っていました。 では、 この箱の下の引き出しの中に黒石が入っている確率はいくらでしょうか?
-
この問題は次のように書き直すことができます。
「 箱A と 箱C のうちどちらかを選んで上の引き出しを開けたところ黒石でした。
箱A を選んだ確率はいくらでしょうか?」
ですから、 この問題は 条件付き確率 を用いて解くことができます。
| 後出来事 | ||||||||||||
| 上黒石 | 上白石 | 計 | ||||||||||
| 先出来事 | 箱A選択 |
|
0 |
|
||||||||
| 箱C選択 |
|
|
|
|||||||||
| 計 |
|
|
1 | |||||||||
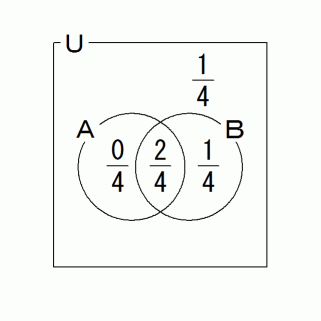
集合A : 箱Aを選んだ
集合B : 上の引き出しに黒石が入っていた
( 集合A または 集合B ) の補集合 : 箱Cを選んだ時に上の引き出しに白石
条件付き確率より、 2分の1 を 4分の3 で割って、 3分の2 が答えになります。 この手の確率のことを、 私は 「 レトロスペクティブ プロバビリティー ( 時系的後ろ向き確率 )」 と言っています。
-
フランチャイズ ドラッグストア では数多くの日用品が安く売られています。 この街には、「 メンズドラッグ 」という店と「 スーパードラッグ 」という店があって隣立しています。「 メンズドラッグ 」は2日に1回の割合で大安売りをしており、「 スーパードラッグ 」は4日に1回の割合で大安売りをしています。 妻も妹も毎日1回どちらかの店に買い物に行っています。 妻は「 メンズドラッグ 」に行く日と「 スーパードラッグ 」に行く日が半々です。 妹は「 メンズドラッグ 」に行く日が「 スーパードラッグ 」に行く日よりも3倍多いと言います。 妻が買い物に行ったときにお店が大安売りをしている確率は、 次の式より求めることができます。
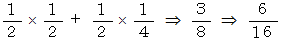
妹が買い物に行ったときにお店が大安売りをしている確率は、 次の式より求めることができます。
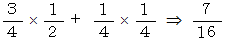
でも、 妹に言わせりゃ大安売りしている確率は 16分の10 とのことです。 なぜなら、 毎朝新聞のチラシをみてから大安売りをしている方の店に行くからです。 両方の店とも大安売りをしていない確率は8分の3らしいのです。
さてここで問題です。 今日、 妻が「 さっき、 ドラッグストアで大安売りの商品を買って得したわ。」と言っています。 妻が今日「 メンズドラッグ 」に行った確率はいくらでしょうか?
| 後出来事 | |||||||||||||
| 安売 | 並売 | 計 | |||||||||||
| 先出来事 | メンズ |
|
|
|
|||||||||
| スーパー |
|
|
|
||||||||||
| 計 | 1 | ||||||||||||
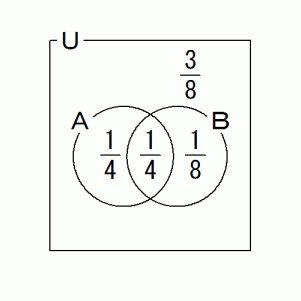
集合A : メンズドラッグに行った
集合B : 安売りをしていた
( 集合A または 集合B ) の補集合 : スーパードラッグに行ったが安売りなし
時系的前向き確率 :
メンズドラッグに行ったときに安売りをしている確率 =
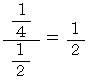
上記の確率ベン図から、 集合Aの補集合の部分を黒く塗りつぶして、
残った範囲を全体とみなして確率を求めます。
スーパードラッグに行ったときに安売りをしている確率 =
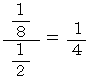
上記の確率ベン図から、 集合Aの部分を黒く塗りつぶして、
残った範囲を全体とみなして確率を求めます。
時系的後ろ向き確率 :
この問題の答え =
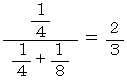
上記の確率ベン図から、 集合Bの補集合の部分を黒く塗りつぶして、
残った範囲を全体とみなして確率を求めます。
-
条件付き確率を理解するためには、 確率ベン図 を利用するといいです。 確率ベン図を利用して時系的後ろ向き確率を求めてみましょう。
時系的後ろ向き確率とは、 Aの先行事象の発生に続いてBの続行事象が発生した時、 Bの続行事象が発生したことが先に発表され、 その時点でのAの先行事象の発生確率はどれだけかを求めるものです。
では問題です。 X と Y の区別のつかない2つの袋があります。 Xの袋には赤玉が1 個と白玉が3個入っており、 Yの袋には赤玉が2個と白玉が2個入っています。 今どちらかの袋を選択し、 その中から玉を1 個取り出したときに赤玉でした。 選んだ袋がXであった確率はいくらでしょうか?
Xの袋を選ぶという事象を集合Aとします。 赤玉が出るという事象を集合Bとします。 そうして確率ベン図を描きます。
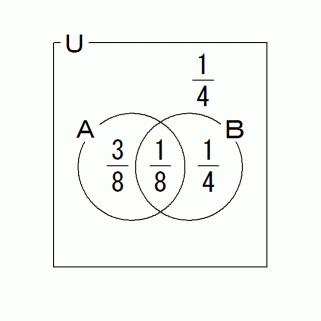
上の図から、 集合Bの補集合の部分を黒く塗りつぶして、 集合Bのみを全体集合とみなします。 すると、 全体の 8分の3 あたりに、 集合Aが占めるのが 8分の1 で、 集合Aの補集合が占めるのが 8分の2 になりますから、 赤玉が出たという情報が得られた時点で、 選んだ袋がXであったという時系的後ろ向き確率は 3分の1 になります。
 確率 へ戻る
確率 へ戻る