( 問い )
-
半径
 、中心角
、中心角 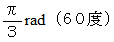 の扇形を下の左の図のように立てて円弧の端を床に接触させ頂点を人差し指で押さえます。 これから円弧を床の上でゆっくりと転がして右図のようになるまで移動させます。 すると、 60度転がります。 さて、 このときの頂点の軌跡はどのようになるでしょうか?
の扇形を下の左の図のように立てて円弧の端を床に接触させ頂点を人差し指で押さえます。 これから円弧を床の上でゆっくりと転がして右図のようになるまで移動させます。 すると、 60度転がります。 さて、 このときの頂点の軌跡はどのようになるでしょうか?

-
高さ
 、 長さ
、 長さ 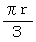 の水平な直線分
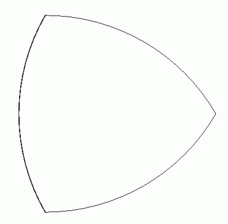
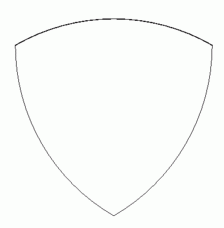
の水平な直線分 の正三角形になります。 そして、 全体としては次のような「 ルーローの三角形 」になります。 このルーローの三角形を時計回りに転がすと、 最も高くなる点の高さは常に
の正三角形になります。 そして、 全体としては次のような「 ルーローの三角形 」になります。 このルーローの三角形を時計回りに転がすと、 最も高くなる点の高さは常に  になります。
になります。A
 B
B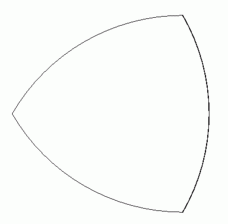
C
 D
D
 上の回転は、 重心の立場からすると、 次のような重心を中心とする回転になります。
上の回転は、 重心の立場からすると、 次のような重心を中心とする回転になります。A
 時計回り60度
時計回り60度  B
B  時計回り30度
時計回り30度  C
C  時計回り30度
時計回り30度  D
D BからDへの過程では、 1つの頂点が床のある点に接触したままの状態が続きます。
BからDへの過程では、 1つの頂点が床のある点に接触したままの状態が続きます。 観察者の立場からすると、 転がりと共に重心も回転します( 正円運動ではありません )ので、 実際の運動は単純な回転ではありません。
観察者の立場からすると、 転がりと共に重心も回転します( 正円運動ではありません )ので、 実際の運動は単純な回転ではありません。 また、 このルーローの三角形を一辺
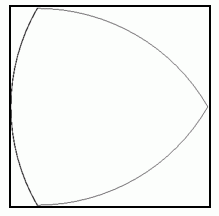
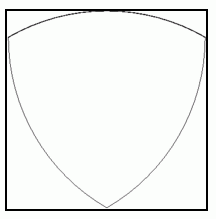
 の正方形の中に入れて回転させると、 絶えず各辺の1点で正方形に内接しながらスムーズに回転します。
の正方形の中に入れて回転させると、 絶えず各辺の1点で正方形に内接しながらスムーズに回転します。A
 B
B 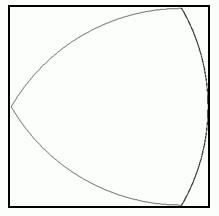
C
 D
D 
 頂点は正方形の辺に接触したまま滑ります。 正方形の角に近づくと、 滑ってきた辺を離れて次の辺へと向かいます。
頂点は正方形の辺に接触したまま滑ります。 正方形の角に近づくと、 滑ってきた辺を離れて次の辺へと向かいます。このとき、 3つの頂点のうちの2つ以上が必ず内接しています。 絶えず各辺の1点で正方形に内接しているということは、 常に正方形をルーローの三角形を含めて5つの部分に分割しているということです。 そして、 このルーローの三角形以外の4つの部分はルーローの三角形の回転によって面積を広げたり狭めたりしますので、 ルーローの三角形は ロータリーエンジン に利用されています。 ロータリーエンジンについて詳しく知りたい方は、 次のサイトをご覧ください。
マツダ ( Mazda ) : http://www.mazda.co.jp/
 その他と物理学 へ戻る
その他と物理学 へ戻る