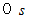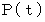２次元平面の原点を通る軌道を、 時刻 に原点を出発して、 速さ で移動していく点 があります。点 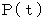の位置ベクトルを 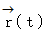とします。 点 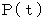における軌道の接線上の点 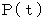の移動方向の単位ベクトル、 つまり、 単位接ベクトルを 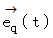とします。 単位接ベクトル 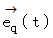に垂直で、 点 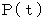の移動方向に近い向きの方の単位ベクトルを 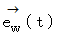とします。

時刻 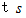における点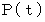 の速さは 　です。 それは次のように表されます。

　　　　

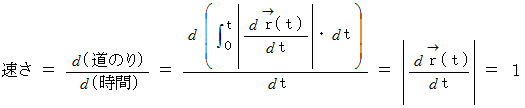
したがって、 次の式が成り立ちます、
　　　　　


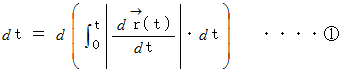
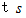　時刻 における点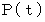 の速度 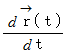　を求めてみましょう。

　　　Ａ． 直線軌道の場合 ：
　　　　　　　　


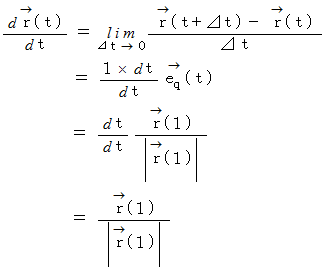
　　　Ｂ． 曲線軌道の場合 ：
　　　　　　　　



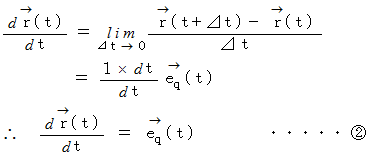
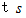　時刻 における点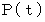 の加速度 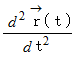　を求めてみましょう。

　　　Ａ． 直線軌道の場合 ：
　　　　　　　　


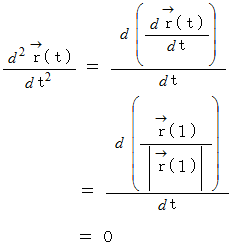
　　　Ｂ． 曲線軌道の場合 ：
　　　　　　　　



に を代入すると、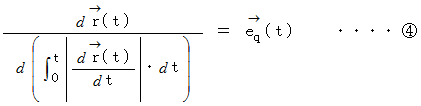
　　　　

　 したがって、 単位接ベクトルは、 位置ベクトルを道のりで微分したものであることがわかりました。 つまり、 道のりが微小に変化したときの位置ベクトルの変化を道のりの微小変化量で割ったものが単位接ベクトルになるということです。


に を代入すると、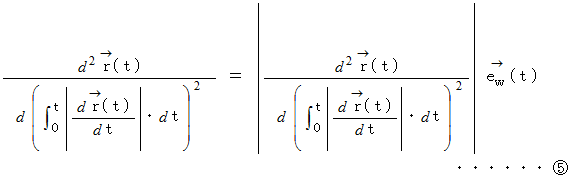
　　　　
　 このベクトルは、 単位接ベクトルを道のりで微分したものです。 つまり、 道のりが微妙に変化したときの単位接ベクトルの変化を道のりの微小変化量で割ったものです。 このベクトルの大きさのことを 点 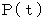における軌道の 「 曲率 」 といいます。 ということは、 曲率とは、 道のりの微小変化による単位接ベクトルの変化を道のりの微小変化量で割ったものの大きさです。 そしてそれは、 その曲線上を速さ で移動し続けている点状物質の加速度の大きさに等しくなっています。 曲率の逆数を 「 曲率半径 」 といいます。



　 これから半径 の円の曲率半径は であることを示します。
原点を中心とする半径 の軌道を、 時刻 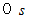に 点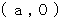 を出発して反時計回りに角速度 で移動する点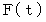 があります。 点 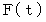の位置ベクトルを 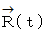とします。 すると、 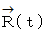は次のように成分表示されます。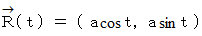
　　　　

道のり ：　 点 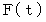は 時間 で 半径 の円周上を ラジアン 回転移動するわけですから、
　　　　　 道のりは 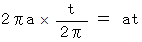です。 したがって、 次のようになります。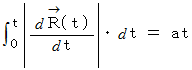
　　　　　　　　　　　

したがって、
　　　　
　　　　

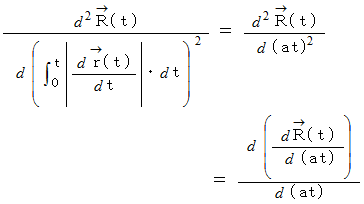
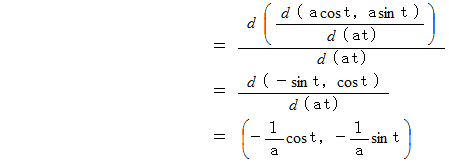
したがって、 円の曲率は次のようになります。
　　　　

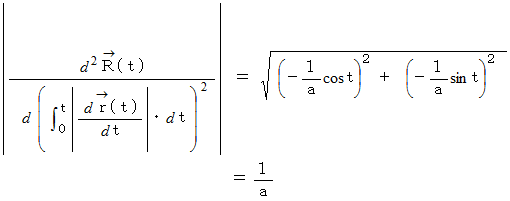
曲率半径は曲率の逆数ですから、 円の曲率半径は であることがわかります。