-
立方体を、現在上になっている面が下にならないようにしながら、重心を通り向かい合う平面に垂直な軸を中心に90度回転することを4回繰り返すすべての場合の数を求めよ。
-
※ 注意: 回転軸は3本あることを、考えている間に忘れないようにしましょう。
「 1回目の回転直後 と 2回目の回転直後 と 3回目の回転直後 に元上面が上側にあるか それとも 前側または後側または右側または左側 にあるか?」のすべての場の数は、2 の3乗 で 8通り。
この8通りについてそれぞれの場合の数を求めてその合計を取ればいい。
→ : 90度回転を表す。
上 : 元上面が上側にあることを表す。
非上下 : 元上面が 前側または後側または右側または左側 にあることを表す。
非下 : 元上面が 上側または前側または後側または右側または左側 にあることを表す。
上 → 上 : 2 通り
上 → 非上下 : 4 通り ( 2+2 )
上 → 非下 : 6 通り ( 2+2+2 )
非上下 → 上 : 1 通り
非上下 → 非上下 : 4 通り ( 2+2 )
※ 注意: 前面を保ったままの回転があることを忘れないこと。
非上下 → 非下 : 5 通り ( 1+2+2 )
上 → 上 → 上 → 上 → 非下
2 × 2 × 2 × 6 = 48 通り
上 → 上 → 上 → 非上下 → 非下
2 × 2 × 4 × 5 = 80 通り
上 → 上 → 非上下 → 上 → 非下
2 × 4 × 1 × 6 = 48 通り
上 → 上 → 非上下 → 非上下 → 非下
2 × 4 × 4 × 5 = 160 通り
上 → 非上下 → 上 → 上 → 非下
4 × 1 × 2 × 6 = 48 通り
上 → 非上下 → 上 → 非上下 → 非下
4 × 1 × 4 × 5 = 80 通り
上 → 非上下 → 非上下 → 上 → 非下
4 × 4 × 1 × 6 = 96 通り
上 → 非上下 → 非上下 → 非上下 → 非下
4 × 4 × 4 ×5 = 320 通り
以上の総計 = 880 通り
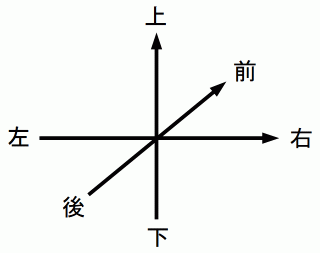
左から右方向 = x 軸方向
下から上方向 = y 軸方向
後ろから前方向 = z 軸方向
注目:
-
私たちは物を観察するときに、目に見える方を「前面」、その反対側を「後面」としますが、 数学的座標的に考えるときは、手前側を「後面」、向こう側を「前面」とした方が間違いが少なくなります。 たとえば、あなたが自宅の玄関のドアを開けて中に入るときは、「今ここの自分」にとって自宅の後側にあるドアを開けて家の中に入ると考えるわけです。玄関というレッテルに捉われてはいけません。 こういった方向の相対的な捉え方は、たとえば「 鏡は前後反転させるだけで、上下反転や左右反転はさせていない。」という真実を納得するときなどに役立ちます。鏡はレッテルに捉われず正直にものごとを映し出しています。
x 軸を中心に右ねじ方向に90度回転することを「前上後下の順回転」ということにしましょう。
x 軸を中心に左ねじ方向に90度回転することを「前上後下の逆回転」ということにしましょう。
y 軸を中心に右ねじ方向に90度回転することを「右前左後の順回転」ということにしましょう。
z 軸を中心に右ねじ方向に90度回転することを「上右下左の順回転」ということにしましょう。
* 外積を意識して並べています。 上か右か前から始めています。
立方体が z 軸を中心に 上右下左の順回転 をすると元の上面は右面になり、立方体が z 軸を中心に 上右下左の逆回転 をすると元の上面は左面になります。
上右下左上右下左上右下左上右下左
順回転では右隣の文字へと変換され、逆回転では左隣の文字へと変換されます。
y 軸を中心: 右前左後右前左後右前左後右前左後
x 軸を中心: 前上後下前上後下前上後下前上後下
 確率 へ戻る
確率 へ戻る