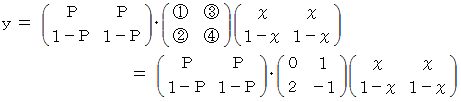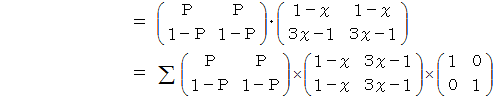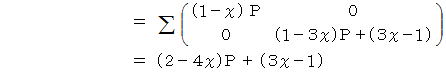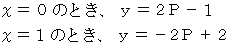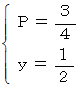|
|
カートはAルート |
カートはBルート |
|
便利屋さんはAルート |
|
|
|
便利屋さんはBルート |
|
|
 確率 へ戻る
確率 へ戻る 大学生のための数学 へ戻る
大学生のための数学 へ戻る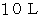 の水を、 Bルートの場合は
の水を、 Bルートの場合は 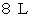 の水を配達することになっています。 それは、 両方で労働の強度がほぼ同じになるようにと、 山荘の主人が配慮してくれたことです。 山荘の主人は、 さらに便利屋さんのことを思って、 毎夕、 山荘の従業員が帰宅するときに、 ゴルフ場で使うカートをどちらかのルートの中腹まで降ろさせ、 翌日に便利屋さんが使えるように準備をしています。 ただし、 どちらのルートに用意されているのかを便利屋さんは聞いてはならないことになっています。 山荘の従業員は、 毎朝、 前の日にカートを降ろした方のルートを通って通勤し、 便利屋さんが使用しなかった場合は、 カートを使用して山荘に戻すことになっています。 また、 山荘の主人はどちらかというとBルートの山水がほしいと思っているので、 Bルートにカートを降ろした時には、 カートにご褒美のバナナとアンパンを用意して、 カートを使用した者が食べてもいいことになっています。 便利屋さんが少しでもラクに山水を配達できる確率を高めるには、 1か月( 30日 )のうち何日 Aルートを通ればいいでしょうか? ただし、 ラクした度合い ( ラクした度 ) を次のような値で表すことにします。
の水を配達することになっています。 それは、 両方で労働の強度がほぼ同じになるようにと、 山荘の主人が配慮してくれたことです。 山荘の主人は、 さらに便利屋さんのことを思って、 毎夕、 山荘の従業員が帰宅するときに、 ゴルフ場で使うカートをどちらかのルートの中腹まで降ろさせ、 翌日に便利屋さんが使えるように準備をしています。 ただし、 どちらのルートに用意されているのかを便利屋さんは聞いてはならないことになっています。 山荘の従業員は、 毎朝、 前の日にカートを降ろした方のルートを通って通勤し、 便利屋さんが使用しなかった場合は、 カートを使用して山荘に戻すことになっています。 また、 山荘の主人はどちらかというとBルートの山水がほしいと思っているので、 Bルートにカートを降ろした時には、 カートにご褒美のバナナとアンパンを用意して、 カートを使用した者が食べてもいいことになっています。 便利屋さんが少しでもラクに山水を配達できる確率を高めるには、 1か月( 30日 )のうち何日 Aルートを通ればいいでしょうか? ただし、 ラクした度合い ( ラクした度 ) を次のような値で表すことにします。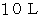 の水を山荘まで運ぶ :
の水を山荘まで運ぶ : 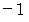
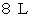 の水を山荘まで運ぶ :
の水を山荘まで運ぶ : 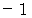
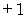
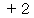
 Aルートを選択し、 カートがあるとき ( Aルートにカートが置いてある ) :
Aルートを選択し、 カートがあるとき ( Aルートにカートが置いてある ) : 
 Aルートを選択し、 カートがないとき ( Bルートにカートが置いてある ) :
Aルートを選択し、 カートがないとき ( Bルートにカートが置いてある ) : 
 Bルートを選択し、 カートがないとき ( Aルートにカートが置いてある ) :
Bルートを選択し、 カートがないとき ( Aルートにカートが置いてある ) : 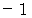
 Bルートを選択し、 カートがあるとき ( Bルートにカートが置いてある ) :
Bルートを選択し、 カートがあるとき ( Bルートにカートが置いてある ) : 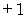
|
|
カートはAルート |
カートはBルート |
|
便利屋さんはAルート |
|
|
|
便利屋さんはBルート |
|
|
 とし、 便利屋さんがAルートを選択する確率を
とし、 便利屋さんがAルートを選択する確率を  とします。 すると、 便利屋さんの 「 ラクした度 」 の期待値は、 次の
とします。 すると、 便利屋さんの 「 ラクした度 」 の期待値は、 次の  で表されます。
で表されます。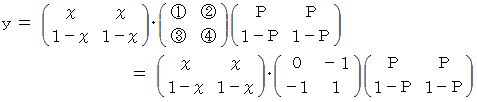
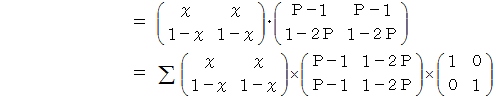
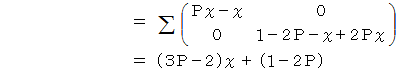
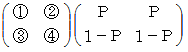 は何をしているのかと申しますと、 便利屋さんがAルートを選択した場合の 「 ラクした度 」 の期待値 と Bルートを選択した場合の 「 ラクした度 」 の期待値 とを求めているのです。 最後に内積をとっているのは、 便利屋さんがAルートを選択する確率にAルートを選択した場合の 「 ラクした度 」 の期待値をかけたもの と、 便利屋さんがBルートを選択する確率にBルートを選択した場合の 「 ラクした度 」 の期待値をかけたもの との合計をとっているのです。 その値
は何をしているのかと申しますと、 便利屋さんがAルートを選択した場合の 「 ラクした度 」 の期待値 と Bルートを選択した場合の 「 ラクした度 」 の期待値 とを求めているのです。 最後に内積をとっているのは、 便利屋さんがAルートを選択する確率にAルートを選択した場合の 「 ラクした度 」 の期待値をかけたもの と、 便利屋さんがBルートを選択する確率にBルートを選択した場合の 「 ラクした度 」 の期待値をかけたもの との合計をとっているのです。 その値 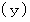 が全体の期待値になります。
が全体の期待値になります。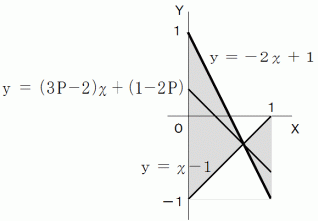
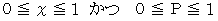 の範囲ですから、
の範囲ですから、 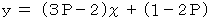 の直線は、 灰色で塗られた範囲内に存在することになります。
の直線は、 灰色で塗られた範囲内に存在することになります。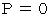 のときです。
のときです。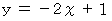 のグラフを見てください。 期待値
のグラフを見てください。 期待値 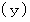 は次のようになります。
は次のようになります。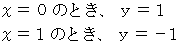
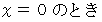 とは、 いつも 「 ラクした度 」 が
とは、 いつも 「 ラクした度 」 が  の場合です。
の場合です。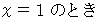 とは、 いつも 「 ラクした度 」 が
とは、 いつも 「 ラクした度 」 が  の場合です。
の場合です。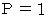 のときです。
のときです。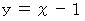 のグラフを見てください。 期待値
のグラフを見てください。 期待値 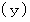 は次のようになります。
は次のようになります。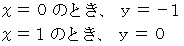
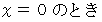 とは、 いつも 「 ラクした度 」 が
とは、 いつも 「 ラクした度 」 が  の場合です。
の場合です。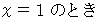 とは、 いつも 「 ラクした度 」 が
とは、 いつも 「 ラクした度 」 が  の場合です。
の場合です。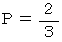 のときは、 便利屋さんの選択の結果に関係なく常に 「 ラクした度 」 の期待値が
のときは、 便利屋さんの選択の結果に関係なく常に 「 ラクした度 」 の期待値が 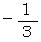 になることもわかります。
になることもわかります。 の値が決まっていません。 そこで
の値が決まっていません。 そこで  のときに
のときに 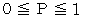 の範囲で
の範囲で  がアットランダムにある値をとったときの 「 ラクした度 」 の期待値を求めてみましょう。 図で、
がアットランダムにある値をとったときの 「 ラクした度 」 の期待値を求めてみましょう。 図で、  のとき、
のとき、  の範囲で
の範囲で  が動くと、
が動くと、 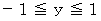 の範囲で
の範囲で  が動くことになります。 ということは、
が動くことになります。 ということは、  のときの 「 ラクした度 」 の期待値は、
のときの 「 ラクした度 」 の期待値は、 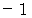 と
と  との中間
との中間  であるということです。
であるということです。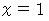 のとき、
のとき、  の範囲で
の範囲で  が動くと、
が動くと、 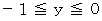 の範囲で
の範囲で  が動くことになります。 ということは、
が動くことになります。 ということは、 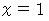 のときの 「 ラクした度 」 の期待値は、
のときの 「 ラクした度 」 の期待値は、 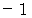 と
と  との中間
との中間 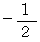 であるということです。 ということは、 「 ラクした度 」 の期待値は、
であるということです。 ということは、 「 ラクした度 」 の期待値は、 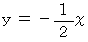 となって、
となって、  の範囲では
の範囲では  のときが最も大きくなります。 そこで、 毎回Bルートを選択する場合が最も 「 ラクした度 」 の期待値が大きくて、 そのときの 「 ラクした度 」 の期待値は
のときが最も大きくなります。 そこで、 毎回Bルートを選択する場合が最も 「 ラクした度 」 の期待値が大きくて、 そのときの 「 ラクした度 」 の期待値は  になると考えますよね。 しかし、 よく考えてみてください。 山荘の従業員だって少しでもラクをしたいのです。 ですから、 「 便利屋さんはどうもBルートばかり選択しているようだ。」 と気づけば、 彼はカートをAルートにばかり置くようになります。
になると考えますよね。 しかし、 よく考えてみてください。 山荘の従業員だって少しでもラクをしたいのです。 ですから、 「 便利屋さんはどうもBルートばかり選択しているようだ。」 と気づけば、 彼はカートをAルートにばかり置くようになります。 座標値が、 最も 「 ラクした度 」 の期待値が大きくなる選択のしかたであり、
座標値が、 最も 「 ラクした度 」 の期待値が大きくなる選択のしかたであり、  座標値がそのときの 「 ラクした度 」 の期待値になります。
座標値がそのときの 「 ラクした度 」 の期待値になります。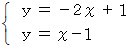
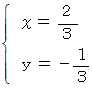
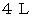 持っていけばよくなり、 「 ラクした度 」 が次のように変わります。
持っていけばよくなり、 「 ラクした度 」 が次のように変わります。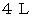 の水を山荘まで運ぶ :
の水を山荘まで運ぶ : 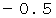
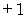
 Aルートを選択し、 カートがあるとき :
Aルートを選択し、 カートがあるとき : 
 Aルートを選択し、 カートがないとき :
Aルートを選択し、 カートがないとき : 
 Bルートを選択し、 カートがないとき :
Bルートを選択し、 カートがないとき : 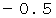
 Bルートを選択し、 カートがあるとき :
Bルートを選択し、 カートがあるとき : 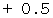
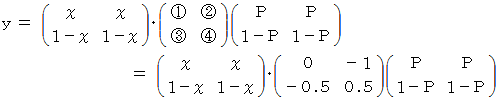
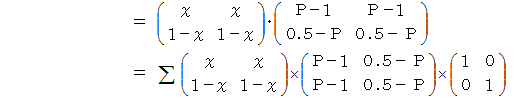
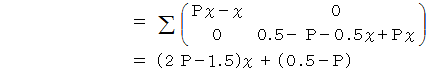
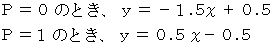
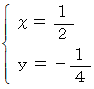
 便利屋さんがAルートを選択し、 カートがあるとき
便利屋さんがAルートを選択し、 カートがあるとき 山荘の従業員は、 Aルートを選択し、 カートはありません。 :
山荘の従業員は、 Aルートを選択し、 カートはありません。 : 
 便利屋さんがAルートを選択し、カートがないとき
便利屋さんがAルートを選択し、カートがないとき 山荘の従業員は、 Bルートを選択し、 カートがあります。 :
山荘の従業員は、 Bルートを選択し、 カートがあります。 : 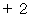
 便利屋さんがBルートを選択し、 カートがないとき
便利屋さんがBルートを選択し、 カートがないとき 山荘の従業員は、 Aルートを選択し、 カートがあります。 :
山荘の従業員は、 Aルートを選択し、 カートがあります。 : 
 便利屋さんがBルートを選択し、カートがあるとき
便利屋さんがBルートを選択し、カートがあるとき 山荘の従業員は、 Bルートを選択し、 カートはありません。 :
山荘の従業員は、 Bルートを選択し、 カートはありません。 : 
|
|
便利屋さんがAルート |
便利屋さんがBルート |
|
山荘の従業員がAルート |
|
|
|
山荘の従業員がBルート |
|
|
 とし、 便利屋さんがAルートを選択する確率を
とし、 便利屋さんがAルートを選択する確率を  とします。 すると、 山荘の従業員の 「 得した度 」 の期待値は、 次の
とします。 すると、 山荘の従業員の 「 得した度 」 の期待値は、 次の  で表されます。
で表されます。