この論文は、 アインシュタインが26歳のときに初めて相対性理論について発表したもので、 日本では「 動いている物体の電気力学 」と訳されています。 この論文は、「 運動学の部 」と「 電気力学の部 」との2部構成になっています。 この論文は、 1988年に内山龍雄によって邦訳され、 さらに解説が付けられ、「 アインシュタイン 相対性理論 」と題して、 岩波文庫の一冊として出版されました。 そこで、 この本を参考にしながら、 この論文の要約を、 行間の意味を含みながら、 光の速さを
 とする単位系を用いて、 私が理解できる範囲内でレポートしてみたいと思います。
とする単位系を用いて、 私が理解できる範囲内でレポートしてみたいと思います。また、 この論文の直後に発表された次の論文では、
 について書かれています。
について書かれています。
この論文のタイトルの日本語訳は「 物体の慣性はその物体の含むエネルギーに依存するか? 」です。 この論文は、 英訳され、 The Principle of Relativity ( Dover 出版 ) に収録されています。 これについても、 最後にその要約をレポートしたいと思います。
このレポートの中で、「 である。」調 で記述した部分は、 私によるアレンジがあるものの、 アインシュタインが論文の中で記述している内容、 または、 言おうとしている行間の意味です。 一方、「 です。 ます。」調 で記述した部分は、 私の解説です。 背景をややピンク色にしています。
定説と若干食い違うところがありますので、 ご了承ください。
ま え が き の 要 約
(1)2つの公理 次の2つの原理により、 私たちは、 静止している電荷に対するマックスウェルの電気力学の理論から出発し、 運動している電荷に対する、 簡単で矛盾のない電気力学に到達することができる。
* アインシュタインが、「 電気力学 」という言葉を用いているのは、
電磁気学の中でも、 とりわけ、 物体を移動させる力を生む電磁場を
意識しているものと思われます。
電磁気学の中でも、 とりわけ、 物体を移動させる力を生む電磁場を
意識しているものと思われます。
 相対性原理
相対性原理等速直線運動をしているどんな座標系でも、 それを基準にとったとき、 ニュートン
力学の法則 と 電気力学の法則 と 光学の法則 は共通の方程式で表される。
 光速不変の原理
光速不変の原理光は、 光源の移動状態に無関係に、一定の速さで真空中を伝わる。
(2)磁石と導体の相対的移動
-
電磁誘導は、 磁石と導体の相対的移動によって生じるのであるが、 この現象を理論的に説明するとき、 磁石に伴走している観察者にとっての内容と、 導体に伴走している観察者にとっての内容とは、 異なるものになる。 前者では、 磁場が導体内の電子に力を作用して、 その結果、 誘導電流が生じるのであるが、 後者では、 電場が導体内の電子に力を作用して、 その結果、 誘導電流が生じる。
(4)「 エーテル 」は存在しない
Ⅰ. 運 動 学 の 部 の 要 約
§1. 同時刻の定義
(1)4次元時空間座標
「 無数の空点には、 それぞれに同期した静止する時計が配置されている。」とアインシュタインは言っているのですが、 彼が言いたかったのは、「 観察者の座標系は、 観察者の座標系の時刻も含めて、 4次元で表される。」ということであろうと思います。 つまり、 次のことを言っていると考えられます。
アインシュタインの言う「 静止系の時刻 : 」とは、「 観察者の座標系の時刻 :
」とは、「 観察者の座標系の時刻 :  」のことですので、
」のことですので、
「 アインシュタインの言う「 静止系の時刻 :
 」とは、「 観察者の座標系の時刻 :
」とは、「 観察者の座標系の時刻 :  」のことですので、
」のことですので、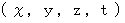 ただし、
ただし、 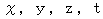 は任意の実数 」で表すことのできる無数の時空点からなる4次元時空間座標が存在する。
は任意の実数 」で表すことのできる無数の時空点からなる4次元時空間座標が存在する。であるから、 また、
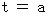 のとき、「
のとき、「 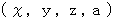 ただし、
ただし、 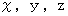 は任意の実 数 」と表すことのできる無数の座標点が存在する。
は任意の実 数 」と表すことのできる無数の座標点が存在する。(2)離れている2点が同時刻であるかどうかを判定する方法
空間的に離れている2つの点Aと点Bが同時刻になっているかどうか判定するためには、 点Aから点Bに向けて光を発射させ、 点Bで光が反射する瞬間の点Bの時刻(
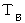 )を観測し、 かつ、 点Aから光を放った瞬間の点Aの時刻(
)を観測し、 かつ、 点Aから光を放った瞬間の点Aの時刻(  )と、 点Aに光が返ってきた瞬間の点Aの時刻(
)と、 点Aに光が返ってきた瞬間の点Aの時刻( 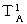 )とを観測し、 次の式が成立するかどうかを調べればいい。
)とを観測し、 次の式が成立するかどうかを調べればいい。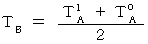
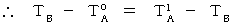
もしこの式が成り立っていれば、 点Aと点Bが同時刻になっていると言える。
ただし、 これには、「 点Aから点Bに光が伝わる時間 」と「 点Bから点Aに光が伝わる時間 」とが等しいという前提条件がついている。 また、 点Aの時刻を観測するには、 点Aで静止している時計を用いなければならないことも明記しておく。
§2. 長さと時間の相対性
(1)長さを計測するための条件
-
その棒の両端を結ぶ直線上を等速直線運動している棒の長さについて考える。
その棒に対しての第0観察者( 棒の伴走者 )が、 同時刻に棒の両端が存在する空点を観測し、 それからその2点の距離を求めて得られるのが、「 静止している観察者にとっての、 観察者に対して静止している棒の長さ 」である。
その棒に対しての第1観察者( 棒に対してその棒の両端を結ぶ直線上を等速直線運動している観察者 )が、 同時刻に棒の両端が存在する空点を観測し、 それからその2点の距離を求めて得られるのが、「 静止している観察者にとっての、 観察者に対して動いている棒の長さ 」である。
これらの棒の長さは異なる可能性がある。
-
まず、 2つの物質Aと物質Bがあり、 それらは共に静止しているものとしよう。 空間的に離れている「 物質Aが存在する空点 」と「 物質Bが存在する空点 」とが同時刻になっているかどうかを判定するためには、 物質Aから物質Bに向けて光を発射させ、 物質Bが光を反射する瞬間の「 物質Bが存在する空点 」の時刻(
 )を観測し、 かつ、 物質Aが光を放った瞬間の「 物質Aが存在する空点 」の時刻(
)を観測し、 かつ、 物質Aが光を放った瞬間の「 物質Aが存在する空点 」の時刻( 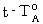 )と、 物質Aに光が返ってきた瞬間の「 物質Aが存在する空点 」の時刻(
)と、 物質Aに光が返ってきた瞬間の「 物質Aが存在する空点 」の時刻( 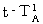 )とを観測し、 次の式が成立するかどうかを調べればいい。
)とを観測し、 次の式が成立するかどうかを調べればいい。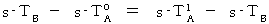
ここで、 静止している2つの物質Aと物質Bとの距離を
 とする。 静止している観察者に対する光の速さは
とする。 静止している観察者に対する光の速さは  であるから、 静止している物質に対する光の「 相対的な速さ 」は
であるから、 静止している物質に対する光の「 相対的な速さ 」は  である。 したがって、 次のようになる。
である。 したがって、 次のようになる。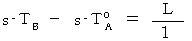 かつ
かつ 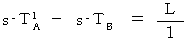
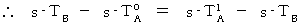
したがって、「 物質Aが存在する空点 」と「 物質Bが存在する空点 」とが同時刻になっていることがわかる。
次に、 2つの物質Aと物質Bがあり、 それらは同じ速度
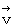 で、 物質Aから物質Bへの方向に移動しているとしよう。 空間的に離れている2つの「 物質Aが存在する空点 」と「 物質Bが存在する空点 」とが同時刻になっているかどうかを判定するためには、 物質Aから光を物質Bに向けて発射させ、 物質Bが光を反射した瞬間の「 そのときに物質Bが存在した空点 」の時刻(
で、 物質Aから物質Bへの方向に移動しているとしよう。 空間的に離れている2つの「 物質Aが存在する空点 」と「 物質Bが存在する空点 」とが同時刻になっているかどうかを判定するためには、 物質Aから光を物質Bに向けて発射させ、 物質Bが光を反射した瞬間の「 そのときに物質Bが存在した空点 」の時刻( 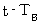 )を観測し、 かつ、 物質Aが光を放った瞬間の「 そのときに物質Aが存在した空点 」の時刻(
)を観測し、 かつ、 物質Aが光を放った瞬間の「 そのときに物質Aが存在した空点 」の時刻( 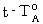 )と、 物質Aに光が返ってきた瞬間の「 そのときに物質Aが存在した空点 」の時刻(
)と、 物質Aに光が返ってきた瞬間の「 そのときに物質Aが存在した空点 」の時刻( 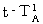 )とを観測し、 次の式が成立するかどうかを調べればいい。
)とを観測し、 次の式が成立するかどうかを調べればいい。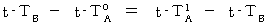
ここで、 速さ
 で移動している2つの物質Aと物質Bとの距離を
で移動している2つの物質Aと物質Bとの距離を 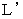 とする。 静止している観察者に対する光の速さは
とする。 静止している観察者に対する光の速さは  であり、 移動している物質に対する光の「 相対的な速さ 」は、 光の伝わる方向と物質の運動方向との関係によって違うから、
であり、 移動している物質に対する光の「 相対的な速さ 」は、 光の伝わる方向と物質の運動方向との関係によって違うから、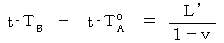 かつ
かつ 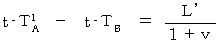
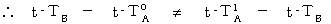
したがって、「 物質Aが存在する空点 」と「 物質Bが存在する空点 」とが同時刻になっていないことがわかる。
さて、「 2つの物質Aと物質Bがあり、 それらは共に静止している。」というのと、「 2つの物質Aと物質Bがあり、 それらは同じ速度で移動している。」というのは、 同一の状況を2人の相対的に移動し合っている観察者たちが観察したときに、 同時にありうる状況である。 ということは、 一方の座標系で、 静止している物質Aと静止している物質Bが同時に破裂したとしても、 他の座標系から見たときは、 移動している物質Aと移動している物質Bは別々の時刻に破裂したことになる。
原文の中では、「 物質 」ではなく「 時計 」になっています。 私が「 物質 」に変更した理由は、「 時刻は空点に宿るものですが、 時計をイメージすると、 時刻が物質に宿るものであると、 勘違いしてしまいやすい。」からです。 時空原点が一致する2つの座標系の相対論的座標変換( ローレンツ変換 )は、「 静止系における、 移動している物質が存在している時所を表す時空点 」から、「 その物質に対して静止している観察者における、 その物質が存在している時所を表す時空点 」への変換であって、「 静止系における、 移動している物質が存在している時所を表す時空点 」から「 静止系における、 移動している物質が持つ 固有の空点 と 固有の時点 」への変換ではありません。
静止系の異なる空点で異なる事件が発生した瞬間の「 静止系の時刻たち 」だけを調べるだけで、「 座標変換による、 2つの異なる空点の同時刻性 の消失 」が説明できるなんて、 とうてい私には思えません。 そこで、 アインシュタインの言っていることが論理的になるよう、 次のように変えてみます。
まず、 2つの物質Aと物質Bがあり、 それらは共に静止しているものとしましょう。 空間的に離れている「 物質Aが存在する空点( 点A )」と「 物質Bが存在する空点( 点B )」とが同時刻になっているかどうかを判定するためには、 物質Aから物質Bに向けて光を発射させ、 物質Bが光を反射する瞬間の「 物質Bが存在する空点( 点B )」の時刻(
 )を観測し、 かつ、 物質Aが光を放った瞬間の「 物質Aが存在する空点( 点A )」の時刻(
)を観測し、 かつ、 物質Aが光を放った瞬間の「 物質Aが存在する空点( 点A )」の時刻( 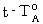 )と、 物質Aに光が返ってきた瞬間の「 物質Aが存在する空点( 点A )」の時刻(
)と、 物質Aに光が返ってきた瞬間の「 物質Aが存在する空点( 点A )」の時刻( 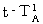 )とを観測し、 次の式が成立するかどうかを調べればいいのです。
)とを観測し、 次の式が成立するかどうかを調べればいいのです。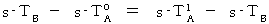
なぜならば、 光が点Aから点Bに伝わる時間を
 とし、光が点Bから点Aに伝わる時間を
とし、光が点Bから点Aに伝わる時間を 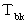 としたときに、 次の式が成り立つからです。
としたときに、 次の式が成り立つからです。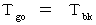
なぜこの式が成り立つかは、 次の理由によります。
静止している2つの点Aと点Bとの距離を
 とします。静止系では光の速さは
とします。静止系では光の速さは  と一定であり、 静止している2つの点に対する光の「 相対的な速さ 」は
と一定であり、 静止している2つの点に対する光の「 相対的な速さ 」は  です。 したがって、 次のようになります。
です。 したがって、 次のようになります。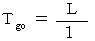 かつ
かつ 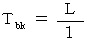
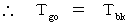
次に、 2つの物質Aと物質Bがあり、 それらは同じ速度
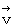 で、 物質Aから物質Bへの方向に移動しているとしましょう。 空間的に離れている「 物質Aが存在する点( 点A ) 」と「 物質Bが存在する点 ( 点B )」とが同時刻になっているかどうかを判定するためには、 物質Aから光を物質Bに向けて発射させ、 物質Bが光を反射した瞬間の「 そのときに物質Bが存在する空点( 点B )」の時刻(
で、 物質Aから物質Bへの方向に移動しているとしましょう。 空間的に離れている「 物質Aが存在する点( 点A ) 」と「 物質Bが存在する点 ( 点B )」とが同時刻になっているかどうかを判定するためには、 物質Aから光を物質Bに向けて発射させ、 物質Bが光を反射した瞬間の「 そのときに物質Bが存在する空点( 点B )」の時刻( 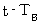 )を観測し、 かつ、 物質Aが光を放った瞬間の「 そのときに物質Aが存在する空点( 点A ) 」の時刻(
)を観測し、 かつ、 物質Aが光を放った瞬間の「 そのときに物質Aが存在する空点( 点A ) 」の時刻( 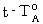 )と、「 物質Aが光を放ったときに物質Aが存在していた空点( 点A ) 」に光が返ってきた瞬間の「 物質Aが光を放ったときに物質Aが存在していた空点( 点A ) 」の時刻(
)と、「 物質Aが光を放ったときに物質Aが存在していた空点( 点A ) 」に光が返ってきた瞬間の「 物質Aが光を放ったときに物質Aが存在していた空点( 点A ) 」の時刻( 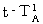 )とを観測し、 次の式が成立するかどうかを調べればいいのです。
)とを観測し、 次の式が成立するかどうかを調べればいいのです。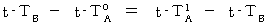
なぜならば、 光が「 物質Aが光を放ったときに物質Aが存在する空点( 点A ) 」から「 物質Bが光を反射したときに物質Bが存在する空点( 点B )」に伝わる時間を
 とし、 光が「 物質Bが光を反射したときに物質Bが存在する空点( 点B )」から「 物質Aが光を放ったときに物質Aが存在していた空点( 点A ) 」に伝わる時間を
とし、 光が「 物質Bが光を反射したときに物質Bが存在する空点( 点B )」から「 物質Aが光を放ったときに物質Aが存在していた空点( 点A ) 」に伝わる時間を 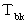 としたときに、 次の式が成り立つからです。
としたときに、 次の式が成り立つからです。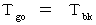
なぜこの式が成り立つかは、次の理由によります。
速さ
 で移動している2つの物質Aと物質Bとの距離を
で移動している2つの物質Aと物質Bとの距離を 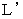 とします。 静止している観察者に対する光の速さは
とします。 静止している観察者に対する光の速さは  ですので、 移動している物質Bに対する光の「 相対的な速さ 」は
ですので、 移動している物質Bに対する光の「 相対的な速さ 」は  よりも小さくなり、 往路の時間は次のようになります。
よりも小さくなり、 往路の時間は次のようになります。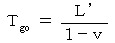
また、 静止している点に対する光の相対的な速さは
 であり、 復路の光の進む距離、 つまり点Aと点Bとの距離は、
であり、 復路の光の進む距離、 つまり点Aと点Bとの距離は、 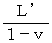 ですので、 復路の時間は次のようになります。
ですので、 復路の時間は次のようになります。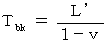
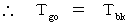
このように、 アインシュタインの言っていることを論理的になるように書き換えますと、 同時刻性の相対性を述べたものではなく、 ただ、 2空点の時刻が等しいかどうかの判定のしかたを述べただけの、 味気ないものになってしまいます。
§3. 静止系から移動座標系への座標変換理論
(1)移動方向と垂直な方向へは、 光の速さは、
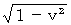 になっている。
になっている。(2) 静止系に対して移動する慣性系の運動方向と垂直な方向の座標は、 座標変換で
変化しない。
(3)ローレンツ変換の導き方
ローレンツ変換の導き方が書いてあるのですが、 私には難しすぎて理解できません。 そこで、 アインシュタインの原論文「 動いている物体の電気力学 」の第2の解説書とも言うべき 風間洋一著「 相対性理論入門講義 」( 培風館1997年 )を参考にさせていただきました。 また、 空間を1次元として考えてみました。
光の運動を観察している第1観察者の時空間座標系を
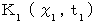 とし、 第1観察者に対してX軸の負の方向に速さ
とし、 第1観察者に対してX軸の負の方向に速さ  で移動している第2観察者の時空間座標系を
で移動している第2観察者の時空間座標系を 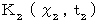 とします。 この2つの座標系は、同じ瞬間に時刻が
とします。 この2つの座標系は、同じ瞬間に時刻が  であり、そのときに空間原点が同じ場所にあるとします。
であり、そのときに空間原点が同じ場所にあるとします。ここで、
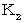 系 にとって
系 にとって 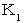 系 の空間原点の空間座標値が常に
系 の空間原点の空間座標値が常に  になるように、 仮想時空間座標系(
になるように、 仮想時空間座標系( 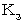 系 )を作ります。
系 )を作ります。 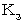 系は次のように表わされます。
系は次のように表わされます。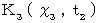 ただし、
ただし、 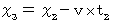
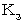 系 は、
系 は、 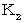 系 と「 時刻 」や「 時間 」や「 空間 」は同じで、「 空刻 」のみが異なります。
系 と「 時刻 」や「 時間 」や「 空間 」は同じで、「 空刻 」のみが異なります。これで準備が整いました。 ではこれから、 アインシュタインの方法で、 ローレンツ変換を導いてみましょう。
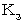 系 から
系 から 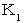 系 に変換してみよう。 座標変換は線形変換であるから、 次のように変換されるとする。
系 に変換してみよう。 座標変換は線形変換であるから、 次のように変換されるとする。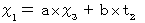 ・ ・ ・ ・(式100)
・ ・ ・ ・(式100)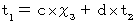 ・ ・ ・ ・(式101)
・ ・ ・ ・(式101)ここで、 第1観察者の座標系において、 時刻が
 の時、 一瞬、 空間原点から光が放出されたとしよう。 そして、 この光は、
の時、 一瞬、 空間原点から光が放出されたとしよう。 そして、 この光は、 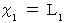 の位置に静止している鏡に
の位置に静止している鏡に 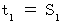 の時刻に反射して、 再び
の時刻に反射して、 再び 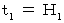 の時刻に空間原点に帰ってきたとする。 つまり、 光が鏡に反射するという事象は、 第1観察者の座標系の時空点
の時刻に空間原点に帰ってきたとする。 つまり、 光が鏡に反射するという事象は、 第1観察者の座標系の時空点 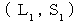 上にあり、 光が空間原点に帰ったという事象は、 第1観察者の座標系の時空点
上にあり、 光が空間原点に帰ったという事象は、 第1観察者の座標系の時空点 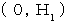 上にあるとする。
上にあるとする。これを第2観察者が見たとき、 光が鏡に反射するという事象は、 第2観察者の座標系の時空点
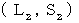 上にあり、 かつ、
上にあり、 かつ、 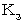 系の時空点
系の時空点 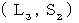 上にあるとする。 また、 光が第1観察者の空間原点に帰ってきたという事象は、
上にあるとする。 また、 光が第1観察者の空間原点に帰ってきたという事象は、 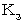 系の時空点
系の時空点 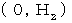 上にあるとする。
上にあるとする。ここで、
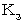 系 において、 光が鏡に到達するまでに実際に移動した距離を
系 において、 光が鏡に到達するまでに実際に移動した距離を  とする。
とする。光の相対的な速さを用いると、 次のような式が成り立つ。
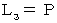
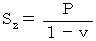
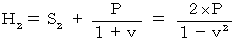
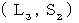 から
から 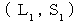 への座標変換は、(式100)と(式101)より、 次のように表わされる。
への座標変換は、(式100)と(式101)より、 次のように表わされる。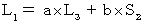
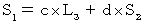
したがって、
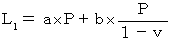 ・ ・ ・ ・(式102)
・ ・ ・ ・(式102)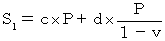 ・ ・ ・ ・(式103)
・ ・ ・ ・(式103)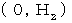 から
から 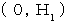 への座標変換は、(式100)と(式101)より、 次のように表わされる。
への座標変換は、(式100)と(式101)より、 次のように表わされる。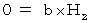
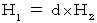
したがって、
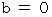 ・ ・ ・ ・(式104)
・ ・ ・ ・(式104)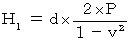 ・ ・ ・ ・(式105)
・ ・ ・ ・(式105)第1観察者の座標系においては、「 光の鏡に対する相対的な速さ 」と「光の空間原点に対する相対的な速さ 」とは等しいので、 次の式が成り立つ。
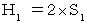
この式に、(式103)と(式105)を代入して、
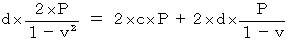
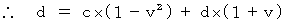
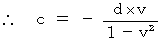
こうして、(式100)と(式101)は、 次のようになることがわかる。
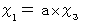
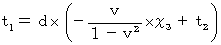
上の式たちに
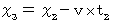 を代入すると、 次のようになる。
を代入すると、 次のようになる。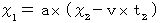 ・ ・ ・ ・(式106)
・ ・ ・ ・(式106)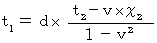 ・ ・ ・ ・(式107)
・ ・ ・ ・(式107)第2観察者が見たとき、 光が鏡に反射するという事象は、 第2観察者の座標系の時空点
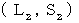 上にある。 このとき、 次の式が成り立つ。
上にある。 このとき、 次の式が成り立つ。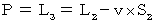
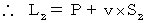 ・ ・ ・ ・(式108)
・ ・ ・ ・(式108)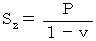 ・ ・ ・ ・(式109)
・ ・ ・ ・(式109)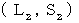 から
から 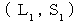 への座標変換は、(式106)と(式107)より、 次のように表わされる。
への座標変換は、(式106)と(式107)より、 次のように表わされる。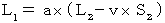
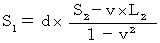
したがって、
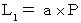 ・ ・ ・ ・(式110)
・ ・ ・ ・(式110)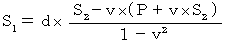
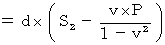
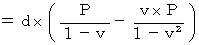
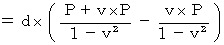
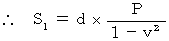 ・ ・ ・ ・(式111)
・ ・ ・ ・(式111)第1観察者が見たとき、 光が鏡に反射するという事象は、 第1観察者の座標系の時空点
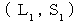 上にある。 このとき、 次の式が成り立つ。
上にある。 このとき、 次の式が成り立つ。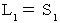
よって、(式110)と(式111)より、 次の式が成り立つ。
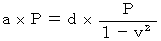
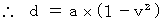
したがって、(式106)と(式107)は次のようになる。
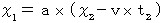 ・ ・ ・ ・(式106)
・ ・ ・ ・(式106)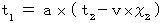 ・ ・ ・ ・(式112)
・ ・ ・ ・(式112)ここで、 空間を2次元に拡張してみる。 第1観察者の座標系において、 時刻
 に、 観察者が静止している空間原点から、 観察者と鏡を結ぶ直線に対して垂直な方向( Y軸とする )に光が放たれ、 その光は、 観察者から
に、 観察者が静止している空間原点から、 観察者と鏡を結ぶ直線に対して垂直な方向( Y軸とする )に光が放たれ、 その光は、 観察者から 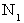 の距離に静止しているもう一つの鏡に、時刻
の距離に静止しているもう一つの鏡に、時刻 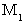 に衝突したとする。
に衝突したとする。これを第2観察者が観察したときに、 光は第1観察者から
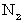 離れて並走しているもう1つの鏡に、 時刻
離れて並走しているもう1つの鏡に、 時刻 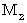 に衝突したとする。
に衝突したとする。すると、
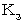 系 では、 光がもう1つの鏡に反射するという事象は、 次の時空点上にあることになる。
系 では、 光がもう1つの鏡に反射するという事象は、 次の時空点上にあることになる。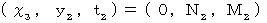 ・ ・ ・ ・ ・(式113)
・ ・ ・ ・ ・(式113)第1観察者のY座標を
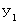 、 第2観察者のY座標を
、 第2観察者のY座標を 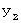 とし、
とし、 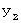 は次のような式に従って
は次のような式に従って 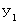 に座標変換されるとする。
に座標変換されるとする。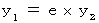
すると、 次のようになる。
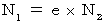 ・ ・ ・ ・ ・(式114)
・ ・ ・ ・ ・(式114)また、(式101):
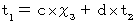 に、(式113)を代入すると、 次のようになる。
に、(式113)を代入すると、 次のようになる。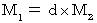
 ・ ・ ・ ・ ・(式115)
・ ・ ・ ・ ・(式115)ここで、 第2観察者の座標系において、 光が移動した時間 = 光が移動した距離 から、 次の式が成り立つ。
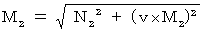
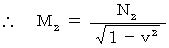 ・ ・ ・ ・ ・(式116)
・ ・ ・ ・ ・(式116)(式116)を(式115)に代入すると、
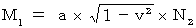 ・ ・ ・ ・ ・(式117)
・ ・ ・ ・ ・(式117)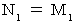 であるから、(式114)と(式117)より、
であるから、(式114)と(式117)より、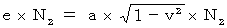
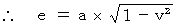
したがって、 次のようになる。
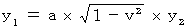 ・ ・ ・ ・ ・(式118)
・ ・ ・ ・ ・(式118)運動系の速度の方向に垂直な方向へは、 速度は空間に対して影響を及ぼさないので、
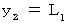 のとき
のとき 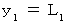 である。 したがって、 次のようになる。
である。 したがって、 次のようになる。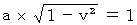
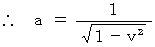
したがって、(式106)、(式112)、 および(式118)は次のようになる。
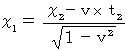
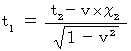
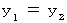
これらが、 静止系から、 静止系に対してχ軸方向に速さ
 で移動している運動系への座標変換式である。
で移動している運動系への座標変換式である。引き続きまして、 後年になってアインシュタインが公開した、 これとは別のローレンツ変換の導き方を紹介します。 それは、 次の本の中に書かれています。
von ALBERT EINSTEIN
1916
* コメント : 金子務により、 2004年に、 この本の邦訳が白揚社から出版さ
れました。「 特殊および一般 相対性理論について 」という本
です。 アインシュタイ自身が相対性理論をわかりやすく解説した
ものを日本語で読むことができ、 相対性理論の理解のための必
読書だと思います。 私もこの本を参考にさせていただきました。
第1観察者の座標系 [ 静止系 ;
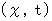 ] における光の運動を表す方程式 :
] における光の運動を表す方程式 :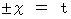
つまり、
 または
または 
速さ
 で移動している慣性系 [ 運動系 ;
で移動している慣性系 [ 運動系 ; 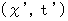 ] における光の運動を表す方程式 :
] における光の運動を表す方程式 :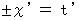
つまり、
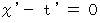 または
または 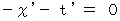
したがって、 光が通過する時空点については、 次の式が成り立つ。
 かつ
かつ 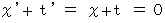
そこで、 座標上のすべての時空点について、 次の式が成り立つと仮定する。
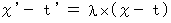 かつ
かつ 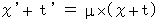
この2つの辺々を加えて、 両辺を2で割ると、
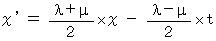
また、 仮定の式の両辺の差をとってから、 両辺を2で割ると、
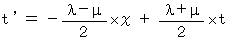
ここで、
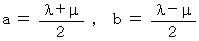 とすると、
とすると、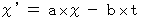 ・ ・ ・ ・(式0301)
・ ・ ・ ・(式0301) ・ ・ ・ ・(式0302)
・ ・ ・ ・(式0302)移動している慣性系の原点は、 常に
 であるので、(式0301)より、
であるので、(式0301)より、移動している慣性系の原点については、 次の式が成り立つ :
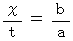 ・ ・ ・ ・(式0303)
・ ・ ・ ・(式0303)また、 静止系の中で移動している慣性系の原点については、 次の式も成り立つ :
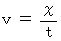 ・ ・ ・ ・(式0304)
・ ・ ・ ・(式0304)(式0303)と(式0304)より、
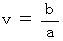 ・ ・ ・ ・(式0305)
・ ・ ・ ・(式0305)さて、 移動している慣性系を静止系と見ることのできる第0観察者を考えよう。
第1観察者の慣性系で距離を求めるためには、 第1観察者の慣性系で同時に2点間の距離を計測しなければならない。 そこで、
 のとき、
のとき、(式0301)より、
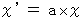
したがって、
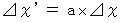 ・ ・ ・ ・ ・(式0306)
・ ・ ・ ・ ・(式0306)第1観察者の慣性系で観測される2点間の距離がいくらであれば、 座標変換により第0観察者の慣性系で
 になるかを求めるためには、(式0306)に
になるかを求めるためには、(式0306)に  を代入すればいい。 すると、 次のようになる。
を代入すればいい。 すると、 次のようになる。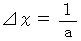
ということはつまり、 第1観察者の慣性系で2点間の距離が
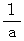 のとき、 それは、 座標変換により第0観察者の慣性系では
のとき、 それは、 座標変換により第0観察者の慣性系では  になる。
になる。第0観察者の慣性系で距離を求めるためには、 第0観察者の慣性系で同時に2点間の距離を計測しなければならない。 そこで、
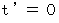 のとき、
のとき、(式0302)より、
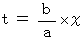 ・ ・ ・ ・(式0307)
・ ・ ・ ・(式0307)(式0307)を(式0301)に代入すると、
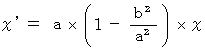
したがって、
 ・ ・ ・(式0308)
・ ・ ・(式0308)第0観察者の慣性系で観測される2点間の距離がいくらであれば、 座標変換により第1観察者の慣性系で
 になるかを求めるためには、 (式0308)に
になるかを求めるためには、 (式0308)に 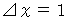 を代入すればいい。 すると、 次のようになる。
を代入すればいい。 すると、 次のようになる。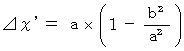
ということはつまり、 第0観察者の慣性系で2点間の距離が
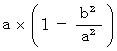 のとき、 それは、 座標変換により第1観察者の慣性系では
のとき、 それは、 座標変換により第1観察者の慣性系では  になる。
になる。ここで、 第1観察者にとっての距離
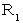 が、 第0観察者の座標に座標変換されて
が、 第0観察者の座標に座標変換されて  になり、 また逆に、 第0観察者にとっての距離
になり、 また逆に、 第0観察者にとっての距離  が、 第1観察者の座標に座標変換されて
が、 第1観察者の座標に座標変換されて  になるとき、 相対性原理により、
になるとき、 相対性原理により、 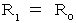 である。 ということは、 次の式が成り立つことになる。
である。 ということは、 次の式が成り立つことになる。 ・ ・ ・ ・ ・(式0309)
・ ・ ・ ・ ・(式0309)(式0305)を(式0309)に代入し、
 を正の実数とすると、
を正の実数とすると、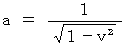 ・ ・ ・ ・ ・(式0310)
・ ・ ・ ・ ・(式0310)(式0310)を(式0305 )に代入すると、
 ・ ・ ・ ・ ・(式0311)
・ ・ ・ ・ ・(式0311)(式0310)と(式0311)を(式0301)に代入して、
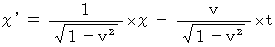 ・ ・ ・ ・ ・(式0312)
・ ・ ・ ・ ・(式0312)(式0310)と(式0311)を(式0302)に代入して、
 ・ ・ ・ ・ ・(式0313)
・ ・ ・ ・ ・(式0313)(式0312)と(式0313)をまとめて、 行列式で表すと、
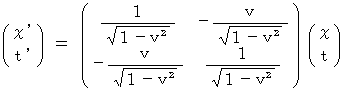
これが、ローレンツ変換式である。
§4. 移動している物質についての、 ローレンツ変換の物理学的意味
(1)移動している物質は移動方向に収縮する
速さ
 で移動している物質は、 移動方向に収縮する。 その割合は、 静止している物質に対して、
で移動している物質は、 移動方向に収縮する。 その割合は、 静止している物質に対して、 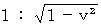 である。 光の速さで移動している物質は、 扁平な形に圧縮されてしまう。
である。 光の速さで移動している物質は、 扁平な形に圧縮されてしまう。(2)移動する時計はゆっくりと時を刻む
速さ
 で移動している時計は、 ゆっくりとしたテンポで時を刻む。 その割合は、 静止している時計に対して、
で移動している時計は、 ゆっくりとしたテンポで時を刻む。 その割合は、 静止している時計に対して、 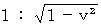 である。
である。では、 ここで問題です。 大気のない地球を想定しましょう。 赤道上に置かれた時計Aと、 風船をつけて空中を漂うようにした時計Bがあるとします。 いま時計Bを、 西に向けて等速運動をさせ、 24時間後に地球を1周して帰ってくるようにします。 では、 2つの時計が再び出会ったとき、 どちらの時計が相対的に遅れているのでしょうか? 地球的見地からすると、 時計Aは静止していて、 時計Bが移動していることになりますが、 太陽系的見地からすると、 時計Bは静止していて、 時計Aが地球の自転の影響を受けて移動していることになります。 また、 銀河系的見地からすると ・ ・ ・ ・ ??
§5. 速度の合成則
(1)相対論的速度合成式
-
第1観察者の座標系のXY平面を等速直線運動している物質Aがある。 そのX成分の速さを
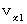 、Y軸成分の速さを
、Y軸成分の速さを 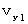 とする。 また、 第1観察者に対して、 X軸の負の方向に速さ
とする。 また、 第1観察者に対して、 X軸の負の方向に速さ 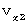 で移動している第2観察者がいる。 このとき、 ローレンツ変換式を用いると、 第2観察者にとっての物質Aの速さを求めることができる。
で移動している第2観察者がいる。 このとき、 ローレンツ変換式を用いると、 第2観察者にとっての物質Aの速さを求めることができる。まず、 第1観察者の座標系で移動している物質の方程式を次のように置く。
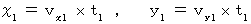
この場合、 第2観察者から第1観察者への座標変換は、 次のローレンツ変換に従う。
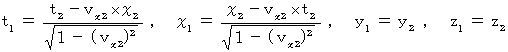
したがって、 第1観察者から第2観察者の座標系に変換すると次のようになる。

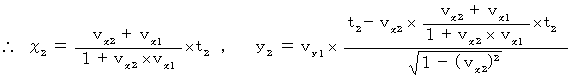
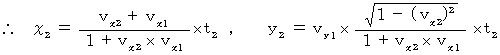
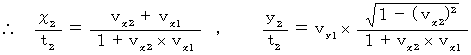
結果は、 この2つの式であり、 X軸方向の速さと、 Y軸方向の速さを表している。
ここで、 上記の2つの式が、 特殊な場合にどのようになるか確認しておきましょう。

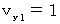 のとき、
のとき、 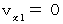 より、 上記の式たちは次のようになります。
より、 上記の式たちは次のようになります。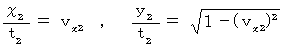

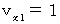 のとき、
のとき、 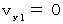 より、 上記の式たちは次のようになります。
より、 上記の式たちは次のようになります。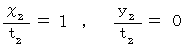

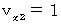 のとき、 上記の式たちは次のようになります。
のとき、 上記の式たちは次のようになります。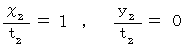

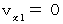 のとき、 上記の式たちは次のようになります。
のとき、 上記の式たちは次のようになります。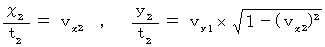
すると、
 より、 光の速さは垂直方向には
より、 光の速さは垂直方向には 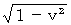 になることがわかります。
になることがわかります。また、
 と
と  より、 第1観察者に対して速さ
より、 第1観察者に対して速さ  の光は、 第1観察者に対してどんな速度で移動している第2観察者にとっても、 速さが
の光は、 第1観察者に対してどんな速度で移動している第2観察者にとっても、 速さが  であることがわかります。
であることがわかります。 ばいおりんのその他の相対論関連論文集 に戻る
ばいおりんのその他の相対論関連論文集 に戻る