次の図は、 記号 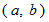が２分岐構造に配置されたものです。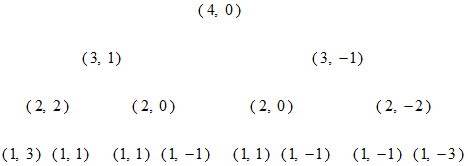

　　　　

同じ記号が何箇所かで使われています。
記号 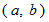の配置の法則は次のようになっています。
　　　　左下に１つ進むと、 は １ 減り、 は １ 増えます。
　　　　右下に１つ進むと、 は １ 減り、 は １ 減ります。


　 さて、 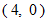から出発し、 上から下へと１つずつ移動します。 そのときに左側を優先します。 訪れた箇所の記号をノートに記入し改行します。 ただし、 記号が既に記入してある場合は記入しません。 そして訪れた箇所には既訪問の印をつけます。 現在いる地点よりも下側に未訪問の箇所が無い場合は、 上へ１つ戻ります。
以上のルールに従ったときに、 最終的にノートには次のように記載されます。

　　　　　　

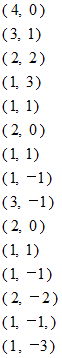
　 この記載法を 「 左順路優先探索順 」 と言うことにします。 この方法は、 一般には 「 深さ優先探索法 」 とか 「 バックトラック法 」 と言われています。 バックトラック法とは、 「 １つずつ手を進められるだけ進めて、 それ以上は無理であるということが解ると一手だけ戻ってやり直す。」 という方法です。


　 次に、 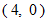から出発し、 上から下へと１つずつ移動します。 そのときに左側を優先します。 訪れた箇所には既訪問の印をつけます。 現在いる地点よりも左下側に未訪問の箇所が無い場合は、 その地点の記号をノートに記入し改行します。 ただし、 記号が既に記入してある場合は記入しません。 現在いる地点よりも下側に未訪問の箇所が無い場合は、 上へ１つ戻ります。
以上のルールに従ったときに、 最終的にノートには次のように記載されます。

　　　　　　

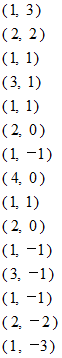
この記載法を 「 左側優先探索順 」 と言うことにします。


　 その次に、 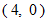から出発し、 上から下へと１つずつ移動します。 そのときに左側を優先します。 訪れた箇所には既訪問の印をつけます。 現在いる地点よりも下側に未訪問の箇所が無い場合は、 その地点の記号をノートに記入し改行します。 ただし、 記号が既に記入してある場合は記入しません。 現在いる地点よりも下側に未訪問の箇所が無い場合は、 上へ１つ戻ります。
以上のルールに従ったときに、 最終的にノートには次のように記載されます。

　　　　　　

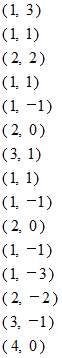
この記載法を 「 左組織優先探索順 」 と言うことにします。


　 最後に、 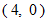から出発し、 上から下へと１つずつ移動します。 そのときに左側を優先します。 訪れた箇所には既訪問の印をつけます。 もし、 行き止まりになったら、 その地点の記号をノートに記入し改行します。 そして上へ１つ戻ります。 そこから再び未訪問の箇所に移動します。 もし、 現在いる地点よりも下側に未訪問の箇所が無い場合は、 上へ１つ戻ってから同様のことを繰り返します。 そして、 行き止まりになっている地点すべてを訪れたら、 行き止まりになっている地点へ繋がる分岐を全て切り落とします。 そして最初から再び同様のことを行います。
　 以上のルールに従ったときに、 最終的にノートには次のように記載されます。

　　　　　　

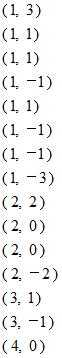
　 この記載法を 「 深さ左優先探索順 」 と言うことにします。


　 非分岐型再帰関数を用いてできる探索順は、 「 左順路優先探索順 」 と 「 左組織優先探索順 」 です。 残念ながら非分岐型再帰関数は 「 左側優先探索順 」 と 「 深さ左優先探索順 」 をすることはできません。

　 この十進BASIC のプログラムでは、 「 深さ左優先探索順 」 をしているように思われるかもしれませんが、 それは出力方法でそう見せかけているだけです。 私の言う 「 深さ左優先探索順 」 とは 「 深さ優先探索法 」 とは異なります。

　 次の十進BASIC のプログラムでも解りますように、 分岐型再帰関数は、 「 深さ左優先探索順 」 以外のすべての探索順をすることができます。

　 たとえば、 「 左側優先探索順 」 を利用したハノイの塔プログラムなんかはすばらしいものです。