(1) 問題 1
-
サイコロを1回ずつ無作為に床に接している辺を軸にして転倒させて移動させ、 そのたびに出た目の数 ( 上になっている面の目の数 ) をチェックする。 これを6回行ったとき、 元の目の数に戻って、 かつ、 すべての目が出る確率はいくらか?
-
上記の条件を満たすときのサイコロの全移動距離を求めなさい? なお、 サイコロの一辺の長さを 1 cm とします。 答えは1つとは限りません。
-
この問題の条件を満たす場合の数は、「 1 から 6 までの自然数をすべて使って6個の数からなる 円順列 を作ったとき、 1 と 6 、 2 と 5 、 3 と 4 のすべてが隣同士になっていない場合の数 」 に等しくなっています。 この条件を満たすような円順列は32通りあります。 また、 サイコロの目の出方の全ての場合の数は、 最初のサイコロの置き方に関係なく 4の6乗 通り になります。 したがって、(1)の答えは 32 を 4の6乗 で割った値 ( 0.78125 % ) になります。 この答えを求めるために、 次のような十進BASIC のプログラムを作ってみました。
出た目の数がすべて異なる場合、 サイコロの移動のパターンは次の例で表されるような2種類に大きく分かれます。 これらの違いは、 横に長いかどうかの違いではありません。 ジグザグに進むか、 3個並んだら隣の行または列に移動するか、 の違いです。
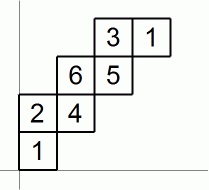
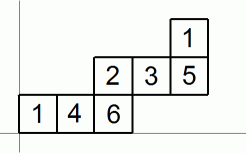
上記の例は、 最初に次の図のようにサイコロが置かれている場合であり、 サイコロの移動を上から観察した図になっています。
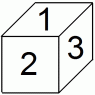
それらの移動距離は、 それぞれ次のようになります。(2)の答えです。
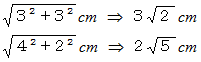
 確率 へ戻る
確率 へ戻る